I learned something new today, and something surprising. I’ve opened up my fair share of bellies and seen intestines doing their slow peristaltic dance in there, and I knew in an abstract way that guts were very long and had to coil to fit into the confined space of the abdominal cavity, but I’d always just assumed it was simply a random packing — that as the gut tube elongated, it slopped and slithered about and fit in whatever way it could. But no! I was reading this new paper today, and that’s not the case at all: there is a generally predictable pattern of coiling in the developing gut, and it’s species-specific.
The midgut forms as a simple linear tube of circular cross-section running down the midline of the embryo, and grows at a greater rate than the surrounding tissue, eventually becoming significantly longer than the trunk. As the size of the developing mid- and hindgut exceeds the capacity of the embryonic body cavity, a primary loop is forced ventrally into the umbilicus (in mammals) or yolk stalk (in birds). This loop first rotates anticlockwise by 90° and then by another 180° during the subsequent retraction into the body cavity. Eventually, the rostral half of the loop forms the midgut (small intestine) and the caudal half forms the upper half of the hindgut (the ascending colon).
The chirality of this gut rotation is directed by left–right asymmetries in cellular architecture that arise within the dorsal mesentery, an initially thick and short structure along the dorsal–ventral axis through which the gut tube is attached to the abdominal wall. This leads the mesentery to tilt the gut tube leftwards with a resulting anticlockwise corkscrewing of the gut as it herniates. However, the gut rotation is insufficient to pack the entire small intestine into the body cavity, and additional loops are formed as the intestine bends and twists even as it elongates. Once the gut attains its final form, which is highly stereotypical in a given species, the loops retract into the body cavity. During further growth of the juvenile, no additional loops are formed, as they are tacked down by fascia, which restrict movement and additional morphogenesis without inhibiting globally uniform growth.
That is just plain awesome. Now I want to open up a zebrafish and look at the curling of its intestines, or better yet, peer into a larva and see if there are any predictable rules of formation. Oh, jeez, I want to look inside my own belly, although that would be a kind of self-defeating experiment.

Morphology of loops in the chick gut. a, Chick gut at embryonic day 5 (E5), E8, E12 and E16 shows stereotypical looping pattern.
b, Proliferation in the E5 (left) and E12 (right) gut tubes (blue) and mesentery (red). Each blue bar represents the average number of phospho-H3-positive cells per unit surface in 40 (E5) or 50 (E12) 10-mm sections. Each red bar represents the average number of phospho-H3-positive cells per unit surface over six 10-mm sections (E5) or in specific regions demarcated by vasculature along the mesentery (E12). The inset images of the chick guts align the proliferation data with the locations of loops (all measurements were made in three or more chick samples). Ant., anterior; post., posterior. Error bars, s.d. c, The gut and mesentery before and after surgical separation at E14 show that the mesentery shrinks while the gut tube straightens out almost completely. d, The E12 chick gut under normal development with the mesentery (left) and after in ovo surgical separation of the mesentery at E4 (right). The gut and mesentery repair their attachment, leading to some regions of normal looping (green). However, a portion of the gut lacks normal loops as a result of disrupting the gut–mesentery interaction over the time these loops would otherwise have developed.
So how do species-specific coiling patterns emerge? A naive expectation might be that there are specific genes associated with the process that selectively impose bends at specific locations along the length of the intestine — that there is genetically determined spatial information along the tube that defines how it should coil. This is not the case. Instead, the reproducible pattern of coiling is an emergent property of some general parameters of the tissues.
You do need to know some very elementary anatomy to know what’s going on here. The gut begins embryonically as a simple, straight tube, fixed at both ends at the mouth and anus. Initially, the gut is the same length as the body, and is suspended from the back of the body cavity by a continuous sheet of tissue, the mesentery, that is also the same length as the gut. But then what happens is that the gut elongates, while the mesentery grows much more slowly. This difference in growth rates means that the gut is under compression along its length, restrained by the mesenteries, which causes it to periodically buckle.
One way to test the role of the mesentery is to remove it. If you carefully cut it away from the gut, as is shown in (c) and (d) of the figure above, it straightens out — in a fully relaxed state, without the compression of the mesenteries, the gut is straight and linear. You can do partial cuts, too, and wherever a stretch of gut is released from the mesentery constraint, it uncoils.
Take it another step. Is this how generic tubes and sheets interact? The authors took a rubber tube of length Lt, and a rubber sheet of length Lm, where Lm is less than Lt. They stretched the rubber sheet to length Lt, stitched it to the rubber tube, and then let it go. Voila, it spontaneously coiled into a configuration (b) that closely resembles the chicken gut (c).
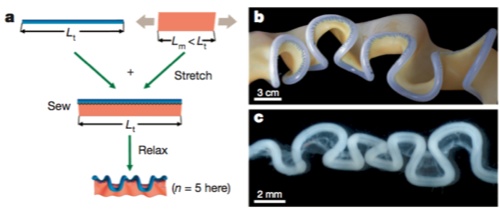
Rubber simulacrum of gut looping morphogenesis. a, To construct the rubber model of looping, a thin rubber sheet (mesentery) was stretched uniformly along its length and then stitched to a straight, unstretched rubber tube (gut) along its boundary; the differential strain mimics the differential growth of the two tissues. The system was then allowed to relax, free of any external forces. b, On relaxation, the composite rubber model deformed into a structure very similar to the chick gut (here the thickness of the sheet is 1.3 mm and its Young’s modulus is 1.3 MPa, and the radius of the tube is
4.8 mm, its thickness is 2.4 mm and its Young’s modulus is 1.1 MPa. c, Chick gut at E12. The superior mesenteric artery has been cut out (but not the mesentery), allowing the gut to be displayed aligned without altering its loop pattern.
This is qualitatively convincing — they do look very similar, and at this point I’m willing to believe that mechanical forces are sufficient to explain the coiling pattern. The authors take another step, though: they bring out the math and get all quantitative. This is a reasonable idea; from the model above, it does look like the shape is reducible to a small number of parameters, so it’s a manageable problem. So brace yourself: a little math coming right up.
We now quantify the simple physical picture for looping sketched above to derive expressions for the size of a loop, characterized by the contour length, λ, and mean radius of curvature, R, of a single period. The geometry of the growing gut is characterized by the gut’s inner and outer radii, ri and ro, which are much smaller than its increasing length, whereas that of the mesentery is described by its homogeneous thickness, h, which is much smaller than its other two dimensions. Because the gut tube and mesentery relax to nearly straight, flat states once they are surgically separated, we can model the gut as a one-dimensional elastic filament growing relative to a thin two-dimensional elastic sheet (the mesentery). As the gut length becomes longer than the perimeter of the mesentery to which it is attached, there is a differential strain, ε, that compresses the tube axially while extending the periphery of the sheet. When the growth strain is larger than a critical value, ε* the straight tube buckles, taking on a wavy shape of characteristic amplitude A and period λ>A. At the onset of buckling, the extensional strain energy of the sheet per wave- length of the pattern is Um∝Emε2hλ2, where Em is the Young’s modulus of the mesentery sheet. The bending energy of the tube per wavelength is Ut∝EtItκ2λ, where κ ∝ A/λ2 is the tube curvature, It ∝ ro4-ri4 is the moment of inertia of the tube and Et is the Young’s modulus of the tube. Using the condition that the in-plane strain in the sheet is ε* ∝ A/λ and minimizing the sum of the two energies with respect to λ then yields a scaling law for the wavelength of the loop:
Did you get all that? If not, don’t worry about it. What it all means is that we can measure general properties of gut tissues, plug the parameters into these formulas, and ask a computer to predict what the gut should look like in a numerical simulation. And it works!

Predictions for loop shape, size and number at three stages in chick gut development. a, Comparisons of the chick gut at E16 (top) with its simulated counterpart (bottom). b, Scaled loop contour length, λ/ro, plotted versus the equivalently scaled expression from equation (3) for the chick gut (black squares), the rubber model (green triangles) and numerical simulations (blue circles). The results are consistent with the scaling law in equation (1). c, Scaled loop radius, R/ro, plotted versus the equivalently scaled expression from equation (4) for the chick gut, the rubber model, and numerical simulations (symbols are as in b). The results are consistent with the scaling law in equation (2). Error bars, s.d.
At this point, you should be saying enough — that’s more than enough awesome to convince you that they’ve determined the rules that shape the gut. But no, they go further: all the above work is in chickens, so they reach out and start disemboweling other species, and ask if their formulas work to describe their gut coiling, too. Would you be surprised to learn that it does?
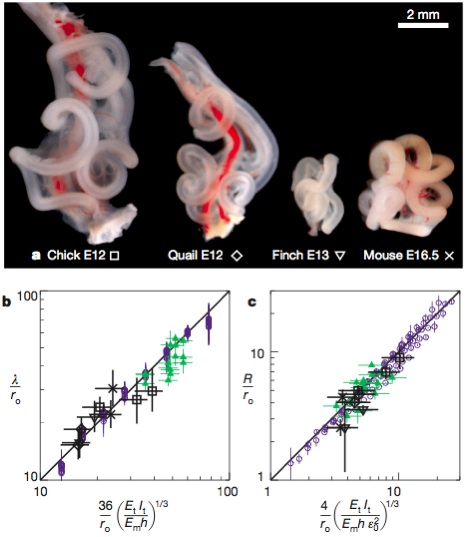
Comparative predictions for looping parameters across species. a, Gut looping patterns in the chick, quail, finch and mouse (to scale) show qualitative similarities in the shape of the loops, although the size and number of loops vary substantially. b, Comparison of the scaled loop contour length, λ/ro, with the equivalently scaled expression from equation (3) shows that our results are consistent with the scaling law in equation (1) across species. Black symbols are for the animals shown in a, other symbols are the same as in Fig. 4b. c, Comparison of the scaled loop radius, R/ro, with the equivalently scaled expression from equation (4) shows that our results are consistent with the scaling law in equation (2) across species (symbols are as in b). In b and c, points are reported for chick at E8, E12 and E16; quail at E12 and E15; finch at E10 and E13; and mouse at E14.5 and E16.5. Error bars, s.d.
What makes this a beautiful result is that it’s a perfect illustration of the principles D’Arcy Wentworth Thompson laid out in his book, On Growth and Form (and even the title of the paper is a nod to that classic of developmental biology). Sometimes, simple mathematical rules govern the patterns we see in developing systems, whether it’s the Fibonacci spirals we see in the head of a sunflower or the coils of a nautilus shell, or tangled loops of our intestines. The form is not laid out in tightly-coded, case-by-case specification in the genome, but by the genetic definition of only a few parameters, in this case the relative rates of growth of two adherent tissues and the compression they impose on an elongating tube, from which a lovely arrangement flowers elegantly.
Savin T, Kurpios NA, Shyer AE, Florescu P, Liang H, Mahadevan L, Tabin CJ (2011) On the growth and form of the gut. Nature 476:57-63.
(Also on Sb)



And then there are tadpoles’ lovely spirals:
Image link from Nat Geo
Guts fold properly, therefore God.
Must be, since it appears to be specified complexity. What, tubes evolve, and continue to develop in a manner that betrays their evolution?
We’re the divine tubes.
Glen Davidson
Clear explanation as always PZ. Now for the proper non-Nat. Geo. site: Fuck off creobots/Idiots.
Okay, now that is just cool. My gut by mysenteric tension.
Science: Explanation of entrail folding.
Christianity: Exposition of entrail fondling.
/@
So, the gut is like a long, thin balloon, and when you blow it up… /snarkasm
But this does remind me of the topology mechanics that say things like phone cords will always frustrate. I wonder if there is a close relation.
Interestingly the model resembles the folding pattern of elastin like proteins above their transition temperature.
With me, it is the light weight 3/8″ diameter coiled water hoses I got for watering the potted plants. I need two to reach all the plants, and I can’t carry them without a bad tangle….
Dhorvath:
Heh, that would make a good nym title: X, mysenterically tense.
Interesting.
From a human point of view, in medicine we were always taught that it develops to roughly the same pattern in everyone; developmental abnormalities include a condition called ‘malrotation’, in which the gut hasn’t gone through its appropriate rotation and positioning.
Saw a baby come in minutes from death once – a big gastrointestinal bleed due to an undiagnosed malrotation.
When the small bowel is obstructed and fills with gas you always see a ladder like pattern on XR:
http://movies-honoratocainelvis.blogspot.com/2011/03/intestinal-obstruction.html
(scroll down to Xrays)
Some variation between individuals, depending on amount of gas, level of obstruction and previous surgery, but it’s a pretty characteristic pattern.
However, discovering how it happens is really impressive.
You go ahead and look inside your own tummy PZ. You’re a teddy bear anyway. It’s just full of soft stuffing.
Just read the full paper… its brilliant. The mathematics of development is beautiful. Papers like that sometimes make me wish I chose maths over ecology.
Now, thanks to you, I too have learned something today. I always love your science posts. You’re a great explainer. I suppose that’s why you’re a professor.
Thank you, this has confused me since embryology in 1975.(still does, but less)
This elegant process does lead to failure, such as:gastroschisis, volvulus, umbilical hernia, internal hernia, the afore mentioned malrotation, genital variations and various others.
Now a designer, would have laid this out in a way, not requiring an alantois evolving from a yolk sack, thus avoiding the above problems, (not to mention the torture of students minds trying to pack the “lesser sack” into three dimensions).
Unless of course the designer is:
Absent
Incompetent
An evil conniving sadistic prick
P.S. MudPuddles …. Just do both
Psst: The link to the original paper is broken, both here and at ScienceBlogs.
This sounds like a fantastic paper, too bad I have to pay. Maybe my university’s computers have access, I’ll have to check next time I’m in. This is a beautiful illustration of the importance of developmental biology to pushing biology further as a field, plus it suggests research opportunities into the differences between species in terms of how cells in the tube versus in the mesentery are responding to growth signals, and I’m curious to know how much this process has to change to adapt to morphological changes as species evolve. Is this something that changes significantly or at all over time or does an appropriate buckling pattern just fall out of the material properties of the tube and mesentery (as the paper seems to suggest according to this summary). It would be really cool if this folding just sort of happens as a matter of course once life had the mesentery figured out, but it’s something that should be looked into.
Also a question for you PZ: Do you think it more likely that some of the earliest bilateria had mesenteries, or that this was this a later adaptation?
re Wholly Cymbal: Not that *I* have any idea, but species differences had BETTER be important, because gut length varies so much between herbivores and carnivores. I wonder what intestine folding looks like in snakes?
Oo! Also, I wondered about frogs (carnivores with a herbivorous tadpole stage) and found this:
Schreiber 2004
re Pteryxx greedily: Yeah, of course, but my query is as to whether these changes in morphology may be adapted to as a matter of course simply by virtue of a differential rate of growth between the mesentery and the gut, or if morphological differences would necessitate the contemporaneous evolution of the signalling involved (protein concentrations etc.). It would be really cool if bilaterians happened to stumble upon a way of fitting guts with a large surface area into their coeloms early on such that mechanical forces just made it “work” regardless of how extreme the morphological changes. I would think this more likely simply because it seems like not having to “worry” about the proper development of the gut could allow for much more morphological flexibility as the clade diversified. The fewer problems to worry about, the easier it is to experiment. Also that would be so cool.
Snakes were the first example that popped into my mind, too, followed by ruminants. How much does this basic idea of “grow the tube fast and the sheet slow” solve for us, do you think?
Will return after reading that paper, looks interesting (though “All of these changes in the anuran intestine are controlled by thyroid hormone” sounds like a big claim).
Yeah, any recoil-type hose or cord is ripe for frustration. Other “lines” just take longer to reach that insanity-inducing level of tangledness.
I knew a guy that had a mal-rotated intestine. They pulled a bunch of it out, gave it a twist or two and put it back in.
You don’t suppose the surgeons have to practise on mal-rotated coiled hoses first?
Wholly Cymbal – I have found that you can nearly always get a copy of an academic paper without paying. Here are the methods:
1. Check the authors’ websites.
2. Ask a person who has access to that journal to email you a pdf. (University staff or students are a good bet, and there are lots here.)
3. Email an author and ask for a copy.
4. If option 1 doesn’t work, try again in 6-12 months. It’s very common that people post their older papers on line.
It would be nice if, after all his complaining about engineers, our host would acknowledge that this gut folding problem is an exercise in structural mechanics. And, because of the simplifications in the excerpted portion of the paper, not a very difficult one.
It should be mentioned, though, that there’s something funny going on when two terms are said to be proportional, but the experimental results are plotted on log-log paper. The authors seem to be trying to cover up some substantial variation between their model and their measurements.
To an engineer, the variation isn’t surprising. Neither of the model’s two linearizing assumptions—that the displacement is small relative to the wavelength, and that the stress is proportional to strain—are met in this problem, so there’s no way to get close agreement between model and experiment. Errors of 50% or so seem perfectly reasonable to me.
The upshot is that guts fold the way they do because they have to. The mechanics of the gut geometry and material properties define the behavior.
@ Cath the Canberra Cook: Thank you, I will definitely try it if the library computers don’t have access or we don’t have a copy of the journal. It never crossed my mind because I can usually find what I’m looking for (usually, finding papers relating to methyl green’s effect on successful cell replication was a bitch, as was finding accessible papers comparing the effects of different detergents on phospholipid vesicles, but other than that it’s been easy going)
Also, @ Pteryxx: the paper you linked to was interesting, especially as my molecular bio is more sharp than my dev bio. I’m having trouble connecting the results (which didn’t seem to suggest anything about species outside of the Anura order, and this is where my ignorance comes in, I don’t even know if the observed and “well documented” shortening of the intestine is unique to this group or something very common in many bilateria) to the results described in PZ’s article in terms of whether these mechanical forces can adapt to morphological changes over generations of species without the need for genetic and developmental-level changes. Still interesting as it seemed, as far as it goes.
@Dr. Drang: I largely agree, though I have always had the impression that PZ’s objections to “engineers” were simply an observation that so many of the ID proponentists seem to have a background in engineering, though I could be wrong. What really strikes me about this is that these developmental biologists really went above and beyond in their search for an explanation. I don’t think these concepts are “engineering concepts” alone, but I agree that there should be acknowledgement of the fact that engineers are responsible for the birth of these ideas (we can always count on engineers for the practical formulae).
“The upshot is that guts fold the way they do because they have to. The mechanics of the gut geometry and material properties define the behavior.”
That’s what I find so exciting. If this is sufficient to adapt to any morphological changes down the road, it could have made for a significant leap in evolvability of the bilateral and, eventually, the tetrapod form.
… I’d always just assumed it was simply a random packing …
Hah! Had your training included proper haruspicy, you’d have been able to foretell future events!
@ Wholly Cymbal: I would assume that a differential rate of growth between intestine and mesentery would be sufficient, and there’s precedent (I think) in limb shape. I was starting to look for existing differences between vertebrate lineages. I admit, so far I’ve only skimmed that anuran paper (darn RL interfering with mah internets) but it seemed like an obvious, extreme vertebrate case. Also, sharks have a bottle-shaped intestine with a spiral valve inside… so somewhere between the aquatic and mammal-bird lineages, began the tube-intestine with a mesenteric fan and the rotation thereof. I’d be interested to see what factors control development of the spiral-valve intestine versus the coiled-tube model.
fyi: Snake GI system photos
and: Manta ray FAQ with intestine diagrams
If both axes are in log scale, and a linear relationship appears, then that relationship will hold on linear axes too.
It is a proportional relationship exactly as the authors said. The use of logarithms on both axes makes it easier to look at data points separated by huge distances without wasting space on the gaps between them. The graph would have to be ten times larger in order to fit everything on at once for those on the left, which makes it hard to examine the pairs side-by-side.
Back when I was still active on my better blog, instead of ranting about politics and religion here, I wrote a few things you might find relevant to your anticipated pleasure of opening yourself and having a look around. Here, and here.
I don’t know if any of you have done any sewing, but precisely this effect and others similar can be achieved while gathering ruffles. This looks like slightly more than a 3:1 ratio (box pleat). A quick search for “ruffles” and “knitting” (’cause it shows the effect better), shows how this is a fairly common phenomena. If you get a strip of lightly woven cloth or non-grosgrain ribbon and carefully pull one of the threads so that the ribbon bunches up around it (the thread here representing the mesentery’s shorter length) you can play along at home!
@Sid Schwab: I remember those fondly, and every time a topic like this comes up, I go read them again. Good to see you.
@Nij: I know that a linear relationship still plots as a straight line on a log-log plot. I also know that log-log plots can make big errors look small. The latter was the gist of my criticism.
And if you look back at the plots, you’ll see that they extend over just one order of magnitude—a range that can be accommodated on a linear plot.