Aperiodic Chevron Tessellation, designed by me

Did you hear?  Someone discovered an aperiodic monotile!  Obviously, these are origami life goals.  And, I’m making it out like a joke, but I’m pretty sure I’m not the only origamist who was thinking that.

Oh, but this origami isn’t the aperiodic monotile.  Instead, I read their paper, and was inspired to create a different aperiodic tiling.  And in the mean time, I learned how an aperiodic tile ticks.

A tiling is a way of covering the entire plane with shapes.  For example, you can tile the plane with squares.  An aperiodic tiling is a tiling that never repeats.  It’s not necessarily difficult to make an aperiodic tiling.  For instance, if I take the square tiling, and I cut some of the squares in half at non-repeating intervals, that’s an aperiodic tiling.

What’s harder to achieve is an aperiodic tile-set.  This is a set of shapes that can tile the plane, but only aperiodically.  This is a bit tricky to prove, because not only do you need to prove that it’s possible to tile the plane aperiodically, you also have to prove that it’s impossible to tile the plane in a repeating pattern.

Many aperiodic tile-sets don’t just consist of a set of shapes, but also have rules about how those shapes are allowed to connect to each other.  Some of these connection rules can be enforced e.g. by making notches on the tiles as if they’re jigsaw puzzle pieces.  But other connection rules are a bit more abstract and can’t be enforced so easily.

The aperiodic monotile discovered by Smith et al. is special because it’s a tile set consisting of only one shape, and no additional connection rules.  I’m going to call it the SMKG tile, named after the initials of the paper authors.  The SMKG tile looks like this:

Fig 1.1. from Smith et al.

I didn’t read the whole paper, but I read enough to get an inkling of why this pattern does not repeat itself.  The authors found that the pieces can be grouped up into several “metatiles”.  There’s the “H” tile, “T” tile, “P” tile, and “F” tile.  Most metatiles consist of multiple SMKG tiles.  Because of the irregular shapes of the metatiles, they obey certain rules about how they can connect to each other.

What’s special, is that when these metatiles are put together, they form even larger meta-metatiles.  These metatiles are again called the “H”, “T”, “P”, and “F” tiles, because they obey the same connection rules as the first set of metatiles.  The pattern repeats at every level.  Metatiles form larger meta-metatiles, form larger meta-meta-metatiles ad infinitum.

Now suppose that we want to check whether the tiling repeats itself after 10,000 tiles.  So we go up the metatile hierarchy until we’re talking about metatiles of size 10,000.  We find that the pattern cannot repeat itself at this scale, because it is not possible to repeat a single metatile over and over again.  So we’ve demonstrated that it is not possible that the tiling repeats after 10,000.  No matter what scale we consider, the tiling cannot fully repeat itself.

The SMKG is not the only aperiodic monotile we know of.  In fact, they discovered a family of aperiodic monotiles, as illustrated below:

Figure 2.3 from Smith et al.

The SMKG tiles are shown third from the left.  My Chevron tessellation is made up of the tiles first on the left.

Technically, the chevron tiling is aperiodic, but the chevron tiles are not aperiodic.  An aperiodic tiling is a tiling that doesn’t repeat.  An aperiodic tile is one that cannot make a tiling that repeats.  It is possible to use the chevrons to make a different tiling that repeats, therefore it is not an aperiodic tile.  But for artistic purposes, we can ignore that, and just consider the aperiodic tiling constructed from chevrons.

I chose to make the chevron tiling because I thought it would be the easiest one to fold with a single sheet of paper.  I have the crease pattern below; as you can see, it’s already complicated enough.

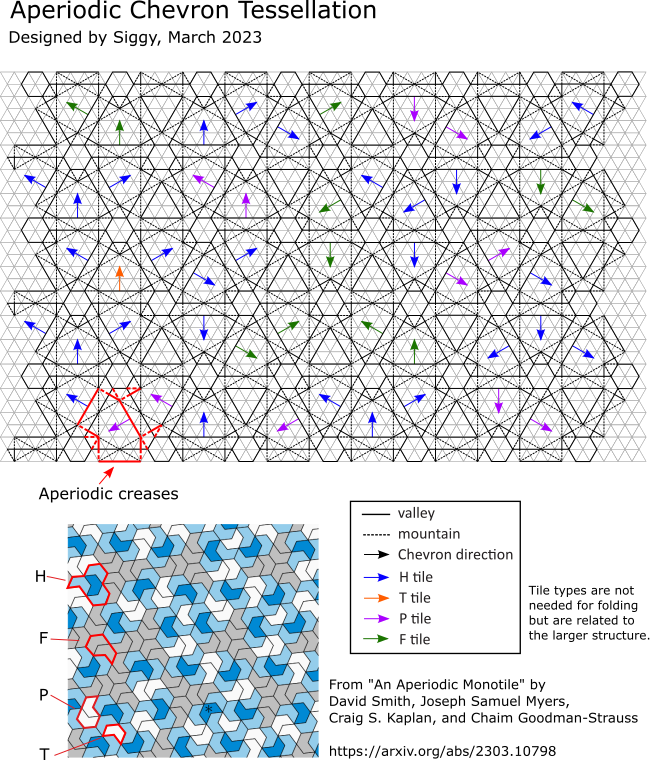
Admittedly this is not the easiest diagram to follow, even if you have experience folding origami tessellations. The arrows are there keep track of which way the chevrons are pointing.