After writing my post on the randomization of a deck of cards, I became more curious about this topic. In a deck of 52 distinct cards, there are 52x51x50…x3x2x1 possible arrangements. This is written in the mathematical notation 52! and is an enormous number. Perfect randomization of a deck means that starting with any given arrangement, after the shuffling process, all possible arrangements are equally likely and have the probability 1/52!. One can also think of it as saying that after the randomization process, a card that started out in any given position should be equally likely to be found in any of the 52 positions.

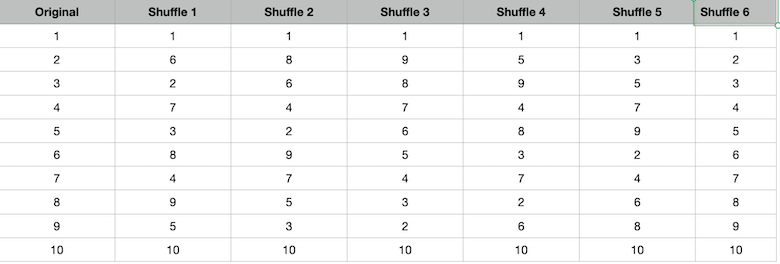
I learned that magicians for some of their tricks use the fact that shuffles do not guarantee randomizing of the deck, and so was curious to see how that might work. To illustrate this very simply, I started with a deck of just ten cards numbered 1 through 10 in order. I then cut the deck in two so that one half contained 1through 5 and the other half contained 6 through 10. Then I imagined a perfect riffle shuffle where the cards from each side are dropped one at a time alternately. You then get the order shown under the heading Shuffle 1.

It does not look obviously ordered but that it is not random can be seen if you cut this deck exactly as before so that the top five are in one hand and the bottom five in the other and do a perfect riffle shuffle again. You then get the result shown in Shuffle 2 which looks a little more disordered. But after the third such shuffle, you see immediately that while cards 1 and 10 are still in the original position, the other eight are perfectly reversed. If you repeat the process yet again you get what is shown in Shuffle 4 which also has a hidden order that is revealed by shuffling again and getting Shuffle 5, where the odd cards make up the top five and the even cards the bottom five. And yet another shuffle gives us back the original order! So the information about the order that we started with never really disappeared with all the shuffling but was just hidden and could be recovered. You can see how magicians could use this knowledge for all manner of card tricks.

This should not be surprising, that when you start with some ordered set and carry out an algorithmic deterministic reversible linear transformation on the data, whet you are doing is merely reordering the set in a systematic way without losing the embedded information. It would be like replacing each letter in the previous sentence with the next letter in the alphabet. The result might look like gibberish but all the original information is still there and recoverable and the science of cryptography is all about how to retrieve information that has been encoded without loss. Randomization means losing information by an irreversible process and that requires any changes to have at least some random component that is irrecoverable. Then information would be truly lost.

Note that the above involved perfect riffle shuffles where only one card drops at a time from each side. This is something that expert magicians can do. Professional card dealers (say in casinos) can get about 80% of perfection while less experienced people can do only 60%.

In my earlier post, I wrote how most people tend to think that riffle shuffling a deck once or twice or even three times is sufficient to randomize the deck when in reality it is not so. Randomizing a deck requires us to deliberately introduce random changes. In normal riffle shuffles, some randomization is introduced because the deck is not cut exactly in half and the cards do not necessarily fall singly from each side. Each shuffle is slightly imperfect and introduces a small random change. This may be why it takes close to a dozen or so riffle shuffles to get close to a truly randomized deck. Many such imperfect shuffles magnify the randomness so that after five or so you just begin to see randomization and that you require at least seven such shuffles to get a rough approximation of a randomized deck.

Inexpert klutzes like me who try to riffle shuffle will often inadvertently drop all the cards on the table (or on the floor) and then have to apologetically pick them up. Oddly enough, that way or by (say) throwing the deck in the air and randomly collecting the cards or by placing them face down on a table and then haphazardly moving cards around with your hands for about a minute to mix the cards (a process that even has a name ‘smooshing’), while looking amateurish, may produce greater randomization than a few expertly executed riffle shuffles.