In the previous post, we had arrived at the seeming impasse concerning the detection of the Higgs particle in that the particles that we can detect (because they live long enough to reach the detectors) are either those that the Higgs does not directly decay into (photons) or have very small probabilities of doing so (electrons and muons). This is because the strength of the interaction between the Higgs particle and any other particle depends upon the other particle’s mass and the photon is massless while the electron and muon are extremely light. (For previous posts in this series, click on the Higgs folder just below the blog post title.)
What we have to do is look at secondary processes, where the Higgs decays into other short-lived particles which then decay into electrons, muons, and photons. This necessarily complicates the analysis but there is no choice. Although we did not know the mass of the Higgs particle, we knew the value of the Higgs field and hence the strength of all the interactions of the Higgs particle with other particles. Hence for any postulated mass of the Higgs particle, we could calculate the probability of it decaying into the various particles that it can decay into. For a Higgs particle of mass roughly 125 GeV, we get the following results: 58% of the time it decays into two bottom quarks; 14% of the time into two W bosons, 6.4% of the time into two tau particles; and 1.6% of the time into two Z bosons. The remaining 20% is spread out over many other ‘channels’, the name given to the final states.
So the particles that are the most copiously produced by the decay of a Higgs are the bottom quarks and W bosons. These (as well as the Z bosons and the tau particles) are also short lived and quickly decay into yet more particles, making the final state consist of a whole slew of particles. There are many final state channels that are possible and the experimenters focus on mainly two of them that make for easier analysis.
One channel is where the Higgs particle first decays into two Z particles, each of which decays into an electron and its antiparticle or a muon and its antiparticle. So the final state that is looked for consists of four charged leptons and no other particles. Another channel is one in which the Higgs first decays into a massive charged particle (say a bottom quark) and its anti-particle, and then each of these emit a single photon before the quark and anti-quark recombine and effectively disappear again, leaving the final state with just two photons and no other particles. These two channels in which there are just those four charged leptons or just those two photons are the ones that are searched for and analyzed.
By measuring the energy and momentum of these final particles, we can reconstruct the properties of the original particle that gave rise to them (if indeed they are the decay products of a single particle) and see if those properties correspond to the properties of the Higgs.
The background problems are immense, the ‘finding the hay in the haystack’ issue I wrote about earlier. As we will see in the next post in the series, there are a huge number of reactions that take place in the proton-proton collisions at the LHC, almost all of them having nothing to do with the Higgs particle. Many of them will produce final states that have the required four charged leptons or the two photons, but they will also have a whole lot more, which makes them not relevant to the search and one has to eliminate those reactions as part of the analysis. There are also many proton-proton collision reactions that can result in the two channels of interest even in the absence of the Higgs particle and this is another source of background noise that has to be accounted for.
What experimenters look for is how many times we would expect to see those two channels if there were no Higgs particles produced as an intermediate state and how many times if the Higgs particles were produced.
Thanks to our knowledge of the strength of interactions between the Higgs particle and the particles it can decay into, we can actually calculate the amount of Higgs particles that we expect to be produced in a proton-proton collision at any given energy for any given mass of the Higgs particle, as well as all the other reactions that can occur without the Higgs being an intermediary particle (i.e., the background). Without the Higgs, we expect the curve to be a smoothly varying function of the total energy of the final state particles. If there is a Higgs, then we expect a slight bump in the data at the energy corresponding to the mass of the Higgs particle. A bump signals the presence of the Higgs and the mass of the Higgs is obtained by seeing which value fits the data best.
In the figures below, we see the results for the two LHC detectors ATLAS and CMS for the particular case when they detect two photons in the final state. The dashed lines are what would be expected if there were no Higgs particle produced and the solid lines are what you would expect if a Higgs particle existed with a mass of 126.5 GeV. The black triangles and circles are the data. (Figures are from the paper Journey in the Search for the Higgs Boson: The Atlas and CMS Experiments at the Large Hadron Collider by M. Della Negra, P. Jenni, T. S. Virdee, Science, vol. 338, p. 1560-1568, 21 December 2012).
ATLAS:
CMS:
While the visual agreement is striking, that is not enough to declare that the search was successful. There is a stringent statistical limit of 5σ (‘five sigma’) that particle physicists impose upon themselves that must be met, signifying that there is 99.99994% confidence or one chance in nearly two million that the result is merely a statistical fluctuation.
This is why they feel confident that this is a real result and not a spurious one, and that the search for the Higgs is over.
Next: Producing the Higgs

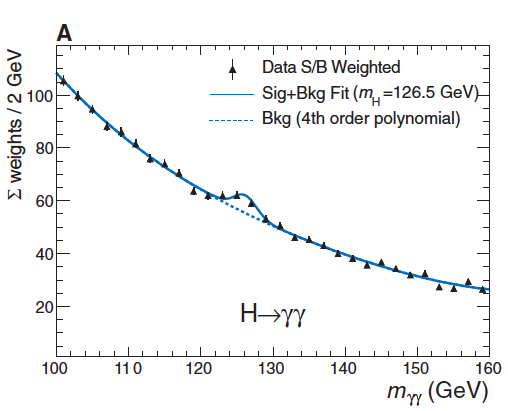
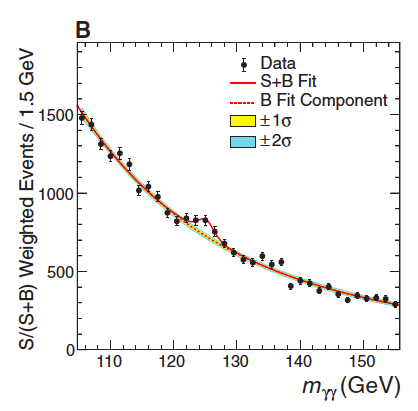
The fit in graph 2 does not look as good around 133-140GeV. It looks like those results are being ignored, is this true? If so what is the criteria used to eliminate certain results. Also the error bars in this region are also quite small which would indicate to me a result that would be less likely to be thrown out.
I am not an expert on what was done in this case but as I understand it, when they do the statistical analysis, they take all the data into account in arriving at the five sigma result. In other words, those seemingly aberrant data are not thrown out but are part of the statistics. If there were a lot of aberrant data, then we would have had lower confidence limits.
Yeah, the statistics has always been a bit foggy for me and also seems to be one of the main criticisms that you run across when discussing the discovery with people. Are there any resources out there that delve more into how they do the statistics? Also would be interesting to know how they decide the size of the energy bins that they are placing results into and also if there is anyway to get greater resolution around the Higgs bump or is there some kind of theoretical or instrument limit on this.
I think you mean “there is 99.99994% confidence that the result is real or one chance in nearly two million that the result is merely a statistical fluctuation”.
Yep, that’s right. I’ll correct it.
In your description of the 2-photon channel you mention the quark and anti-quark “recombining”: is that something to be distinguished from “annihilation”, as you seem to imply that no other decay products would come out (certainly no photons)? Or is the whole process essentially an expansion of the ‘annihilation process’?
Love the series by the way!
It is the same as annihilation.
Glad you like the series!