Things have gotten quiet over here, due to SIGGRAPH. Picture a giant box of computer graphics nerds, crossed with a shit-tonne of cash, and you get the basic idea. And the papers! A lot of it is complicated and math-heavy or detailing speculative hardware, sprinkled with the slightly strange. Some of it, though, is fairly accessible.
This panel on colour, in particular, was a treat. I’ve been fascinated by colour and visual perception for years, and was even lucky enough to do two lectures on the subject. It’s a ridiculously complicated subject! For instance, purple isn’t a real colour.
Ok ok, it’s definitely “real” in the sense that you can have the sensation of it, but there is no single wavelength of light associated with it. To make the colour, you have to combine both red-ish and blue-ish light. That might seem strange; isn’t there a purple-ish section at the back of the rainbow labeled “violet?” Since all the colours of the rainbow are “real” in the single-wavelength sense, a red-blue single wavelength must be real too.
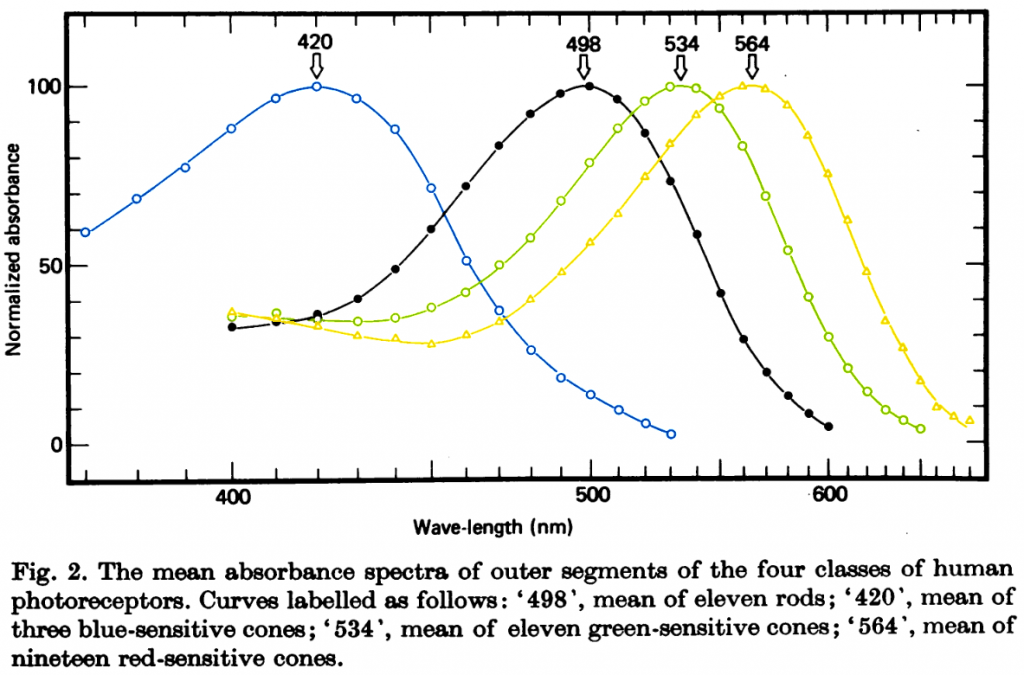
It turns out that’s all a trick of the eye. We detect colour through one of three cone-shaped photoreceptors, dubbed “long,” “medium,” and “short.” These vary in what sort of light they’re sensitive to, and overlap a surprising amount.
Your brain determines the colour by weighing the relative response of the cone cells. Light with a wavelength of 650 nanometres tickles the long cone far more than the medium one, and more still than the short cone, and we’ve labeled that colour “red.” With 440nm light, it’s now the short cone that blasts a signal while the medium and long cones are more reserved, so we slap “blue” on that.
Notice that when we get to 400nm light, our long cones start becoming more active, even as the short ones are less so and the medium ones aren’t doing much? Proportionately, the share of “red” is gaining on the “blue,” and our brain interprets that as a mixture of the two colours. Hence, “violet” has that red-blue sensation even though there’s no light arriving from the red end of the spectrum.
To make things even more confusing, your eye doesn’t fire those cone signals directly back to the brain. Instead, ganglions merge the “long” and “medium” signals together, firing faster if there’s more “long” than “medium” and vice-versa. That combined signal is itself combined with the “short” signal, firing faster if there’s more “long”/”medium” than “short.” Finally, all the cone and rod cells are merged, firing more if they’re brighter than nominal. Hence where there’s no such thing as a reddish-green nor a yellow-ish blue, because both would be interpreted as an absence of colour.
I could (and have!) go on for an hour or two, and yet barely scratch the surface of how we try to standardize what goes on in our heads. Thus why it was cool to see some experts in the field give their own introduction to colour representation at SIGGRAPH. I recommend tuning in.