There is a magic and arbitrary line in ordinary statistical testing: the p level of 0.05. What that basically means is that if the p level of a comparison between two distributions is less than 0.05, there is a less than 5% chance that your results can be accounted for by accident. We’ll often say that having p<0.05 means your result is statistically significant. Note that there’s nothing really special about 0.05; it’s just a commonly chosen dividing line.
Now a paper has come out that ought to make some psychologists, who use that p value criterion a lot in their work, feel a little concerned. The researchers analyzed the distribution of reported p values in 3 well-regarded journals in experimental psychology, and described the pattern.
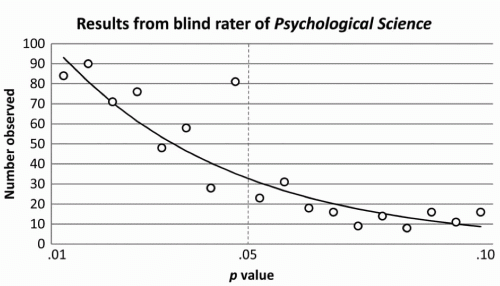
Here’s one figure from the paper.
The solid line represents the expected distribution of p values. This was calculated from some theoretical statistical work.
…some theoretical papers offer insight into a likely distribution. Sellke, Bayarri, and Berger (2001) simulated p value distributions for various hypothetical effects and found that smaller p values were more likely than larger ones. Cumming (2008) likewise simulated large numbers of experiments so as to observe the various expected distributions of p.
The circles represent the actual distribution of p values in the published papers. Remember, 0.05 is the arbitrarily determined standard for significance; you don’t get accepted for publication if your observations don’t rise to that level.
Notice that unusual and gigantic hump in the distribution just below 0.05? Uh-oh.
I repeat, uh-oh. That looks like about half the papers that report p values just under 0.05 may have benefited from a little ‘adjustment’.
What that implies is that investigators whose work reaches only marginal statistical significance are scrambling to nudge their numbers below the 0.05 level. It’s not necessarily likely that they’re actually making up data, but there could be a sneakier bias: oh, we almost meet the criterion, let’s add a few more subjects and see if we can get it there. Oh, those data points are weird outliers, let’s throw them out. Oh, our initial parameter of interest didn’t meet the criterion, but this other incidental observation did, so let’s report one and not bother with the other.
But what it really means is that you should not trust published studies that only have marginal statistical significance. They may have been tweaked just a little bit to make them publishable. And that means that publication standards may be biasing the data.
Masicampo EJ, and Lalande DR (2012). A peculiar prevalence of p values just below .05. Quarterly journal of experimental psychology PMID: 22853650


Hmmm – that is worrying. Psychological Science did suggest that contributors report Prep (the probability of replication; the “rep” should be formatted as subscript), rather than p values, but that suggestion/requirement seems to have disappeared from the author guidelines.
“There are lies, damned lies, and statistics.” – Samuel Clemens.
“I get by with a little help from my adjustments.”
Glen Davidson
Even if everything was above board, every one in twenty ‘significant’ results would be a fluke
I don’t think this is a big deal for social “science”, and I bet it happens lots elsewhere. When keeping your job depends on getting statistical significance, don’t be surprised when things emerge as significant.
I say it doesn’t matter because it ignores the fact that unless an effect is replicated, it will not impact the field (at least not long term). And, p values become irrelevant when effects are replicated; we instead focus on effect sizes.
Most of the stuff we publish never gets cited. So, by definition, most studies have zero impact on the field. Effects that impact the field do so at least because they are reliable (among other things).
I think you are making the mistake that smaller p values mean bigger effects. They do not (run 1000s of subjects and it’s not uncommon to get worthless effects with p < .0001). It's all about effect sizes on replicated results.
So, playing the p value game might get your next article published, but unless the effect is real, it's not going to impact the field.
Wow. I’ve had a few p-values in my own research come out at 0.040-0.049 just on their own without “cheating” or throwing out outliers.
Sucks to have those regarded suspiciously, but I see what you mean with that big spike.
On the other hand, I’ve had people in some fields like Landscape Ecology (not my branch of Ecology) tell me that a lot of them accept p = 0.10. Is 90% certainty that your results are not an accident good enough? As you say, it’s an arbitrary standard.
While it’s bad that bias is being introduced to the work, there’s obviously no practical difference between p=.051 and p=.049, it just makes it cross the line. Improper and unethical? Certainly. Meaningful? Not really. p=.05 is good for a lot of things, but if you really want to be certain of your results when it’s critical to do so, you’re looking for .01 or .005
Unfortunately, P. Z. has gotten the definition of statistical significance wrong.
P value is not the probability that your results can be accounted for by accident.
P value is the probability of obtaining the results, or more extreme results, given that the null hypothesis is true.
See for instance Douglas G. Altman’s “Practical Statistics for Medical Research” (1999), p. 167 or A. J. Underwood’s “Experiments in Ecology” (2009) p. 56.
This shows that even expert professors in biology sometimes get statistics wrong and counts toward the more general point that p values are often misunderstood and should, at bare minimum, be replaced by effect size and confidence intervals.
#7
Lower p values do not mean bigger or more certain effects.
Even worse, the creationists are going to jump on this and scream about how science is unreliable.
I think bryanpesta’s comment (#5) above is poignant though. Sure, you might get that paper published but findings that have high impact are going to be the repeatable, large effects.
@emilkarlsson: Yes, but I think PZ was using a sort of shorthand.
@kp71 that is probably true and I did not mean to make it sound so aggressive. It is just that the precise formulation he happen to make is a common misconception.
Call it a nitpick, if you will.
It’s not a bad nit to pick.
This is true, but the most common null hypothesis used in most science experiments is that there is no difference between groups and any observed differences are due to accident/random fluctuations.
Notice also that if your experiment looks at, say 20 or more variables for comparison at the same time, given a null hypothesis of no difference, you will observe a difference in at least one variable with a p-value < 0.05 most of the time. Though there is a second statistical adjustment you can make to account for this, and a good reviewer will make sure you have made it already.
Maybe*. But this may also be the result of bias in reporting. Most results are never published because they aren’t significant, which is precisely what the curve explains*. People are not even likely to report p-values greater than 0.05. If most results are insignificant, than the great proportion of significant results will hover around 0.05. Further, people always report highly significant results (near 0.01) which would boost the proportion of these, even though they should be the rarest of all results reported.
Notice, also the sawtooth pattern (alternating high and low among points). What the fuck is that about?
*Until I get to read the paper, which may not happen soon, I will assume that studies using Bonferroni-correction in assessing significance were discounted.
Anyway, any Bayesians around want to take this opportunity to deliver a blow to the guts of frequentism?
The chance doesn’t come often.
There is little doubt that the experimental psychology literature is rife with false results due to the combination of statistical shenanigans like significance chasing and selective reporting, and institutionalized publication bias (ie, official policies of journals to only publish statistically significant findings). One example I detected and blogged about was the study “Analytical Thinking Promotes Religious Disbelief” by Gervais and Noranzayan, which was published recently in Science. A number of atheist bloggers picked up on the study, which claimed to show that prompts as subtle as having subjects look at a picture of Rodin’s The Thinker reduced their degree of religious belief. The paper included the results of four experiments, each of which was significant by a suspiciously small margin (p-values of .03 or .04). I conducted the test by Ioannidis for excess significance on the results and indeed found evidence of inflated significance. Details are on my blog.
On a related note, we should in general be wary of p-values in the range of .05 to .01. Bayesian results show that p-values in this range often do not favor the alternative hypothesis over the null hypothesis strongly or at all, and can even favor the null hypothesis over the alternative.
Jay
Strictly speaking, it’s also possible that some of these studies are simply presenting weaker conclusions than originally sought.
For example, suppose I decide to study the correlation between obesity and conservatism. (As I recall, such a correlation was shown to exist not too long ago, although I could be mistaken and I’m certainly making up the numbers here.) I go out and get people to fill in surveys and weigh them as well. I end up with a list of numbers linked to political preferences. When I group the political preferences together in a way to categorize people as “Strongly Liberal”, “Liberal”, “Centrist”, “Conservative”, and “Strongly Conservative”, I can then issue a wide range of statements about weight which have varying levels of certainty. (So, for example, I might say with 97% certainty that the mean of the distribution of right-of-centrist weights is at least 15 pounds overweight, or with 95% certainty that the mean is at least 20 pounds overweight, or with 90% certainty that the mean is at least 30 pounds overweight, etc.) I can then look for which statement will give me p < 0.05, and publish that one.
This, assuming it occurs, is still entirely valid. Whether this type of study is done often enough to produce an outlier on the graph I don’t know.
If you’re doing closely controlled lab experiments with huge sample sizes, you’d better show me 0.01 or better. If you’re doing field studies and making difficult measurements of real traits with lots of real variation, I’m willing to look at 0.10 or even 0.15, And for the kinds of questions I’m asking, if I can’t clearly see the effect in the graphs then I don’t care about the P anyway. I have published several studies using ANOVA and ANCOVA and never used the term ‘significant’ once; just reported the Ps.
You may be wondering , jt512, how I knew what you were typing before it had posted.
I had foreseen it.
Thou shalt obey the Third Statistical Commandment of John Alroy:
http://www.nceas.ucsb.edu/~alroy/JA_commandments.html
Antiochus (#20), I thought you were going to cite Daryl Bem’s “Feeling the Future”, which has become the canonical case of significance by shenanigans in experimental psychology.
jt512:
I guess you were wrong. However, I knew you’d cite it.
[Just kidding…cool blog!]
@jt152
I just wanted to say a big thank you for your blog post. I actually JUST used that paper in a grant application, so it has made me slightly concerned. Fortunately, that paper was not really central to our proposal and was more an example of how intuitive versus heuristic thinking could potentially be induced (As in, these are what OTHER people are looking into, versus what we would like to do).
Although I have also heard that both Science and Nature publications are actually quite poor on their stats
@ChasCPeterson
My first lab job was making up solutions in an analytical chem labs, running samples through AAS, etc. If you got an r squared value of less than 0.9999 on your standards curve, you screwed up somewhere. Next lab job was working in an forestry ecology lab. P-values were usually in the 0.05 to 0.2 range, but it was percent of variation that really mattered, especially over multiple field seasons. A “weak” signal (i.e. high p values) but appearing in every data set from multiple field sites and field seasons, that is something you can take to the publisher.
@Amphiox #14: the point from post 8 is valid. The p-value is the probability that you get a result as extreme or more extreme as the observed one under the assumption that the null hypothesis is true.
However, “can be accounted for by chance” is always true as long as the p-value is not literally zero. Therefore the interpretation of the statement is unclear and in my view unfortunately rather close to the common misconception that the p-value is the probability of the null hypothesis being true.
As the post itself shows it is important to get these statistical concepts right.
@Ananworsley: Thank you, but if I had written a letter to the editor of Science like I should have, I might have saved you from citing a dubious paper.
I agree that some of this is probably pressure to produce at work. Because of the conditions which social science is forced to perform under (we can’t really imprison people to get isolation in the testing process and the biases of the researcher and/or the audience are a significant factor, even with blinds), the threshold for significance is higher than that in the sciences which can more readily isolate their experiments.
In the case of statistics in the social sciences, rigor is greatly dependent on the schools; I’ve seen people get an education in statistics who essentially memorized the formulas and called it a day, which is supremely unproductive for the amount of variation you’ll get in situations which are being studied in the social sciences. I’m guessing, in those cases (and because I’ve seen people talk themselves into discarding outliers altogether, instead of including them and offering probable correlative effects for those outliers, as well as analysis with and without the outliers), that the statistical inflation is a function of poor stats literacy and that pressure to produce.
It is increasingly difficult to be published in the social sciences, and because you need publications to do anything in the field, I’m not actually surprised at the fudging. Of course, Fanelli published a paper in 2009 suggesting that up to 72% of the scientists she surveyed stated that they had observed their colleagues using questionable research practices, and 33% confessed that they had done so themselves. Mind you, the sample was too small for my taste, but as a sort of advance survey, it points to a problematic trend. The most likely scientists to engage in questionable practices were those in the medical/pharmacological industries.
It’s not just the social sciences with that pressure to publish and stats principles illiteracy.
BryanPesta: Fuck you.
@15: Further, people always report highly significant results (near 0.01) which would boost the proportion of these, even though they should be the rarest of all results reported.
That’s likely not going to be the case unless you are simply fishing for data. A lot to most experiments are designed with the goal of getting positive results. What’s being described as a publication bias could at least in part be an experimental design bias (i.e., you design experiments that have a high probability of statistical significance). I’m still surprised that the highly significant (0.01) reports are so highly reported. Maybe we’re answering questions we already know the answers to?
If the cut off point for publication is set at 5% – I would expect a spike at just under that point. Not necessarily by fudge factor but simply selection bias.
.001 sun comes up in east…not interesting
.5 sometimes when flipping coins with your thumb it is heads…not interesting
.05 that this here effect is something true…that is interesting.
mouthyb:
I can’t speak for all of the social sciences, but experimental psychology journals have institutionalized the practice of publication bias by making it almost impossible to publish negative (ie, null) results. This is not the case in the biomedical sciences, where the importance of null findings is better understood.
Institutionalizing publication bias in a field has a profound effect on the body of literature in that field. Imagine a field in which all null hypotheses studied are true and which only publishes statistically significant findings. Then, the 95% of experiments in the field with true negative findings are never submitted for publications, while the 5% with false positive findings are published. Therefore, all the papers in the field reporting original findings will be false.
But it gets worse. Since null findings are never published, null replication attempts are never published. Therefore, false studies are never refuted. But it gets worse yet: Some replication attempts will themselves be “successful”—ie, they will be false positives themselves—and will be published. Therefore, the field will eventually develop a body of “knowledge”—things that are generally accepted to be true because they’ve been replicated—that will be entirely false.
I have to wonder how close to this scenario the field of experimental psychology is. That is, how much of what is considered to be generally accepted knowledge in experimental psych is built on a foundation of false positive results.
I wish it was common practice to report the actual p value, instead of simply looking for p < 0.05.
A p value of 0.06 should be treated pretty much exactly like p = 0.05. The statistical difference in that case is insignificant.
#32
Significance is a binary decision. .04 is just as significant as .00001. Putting adjectives on p-values is wrong.
Cumming (2008) likewise simulated large numbers of experiments …
(S)He did an experiment by simulating experiments … uh, what color of pill was involved?
Notice that unusual and gigantic hump in the distribution just below 0.05?
Non-scientist here, trying to understand this. By “below” our esteemed host means “to the left of”, right? It’s all over my head!
jt512: I’m going to guess some of that is competition due to economic factors, as well. The ‘harder’ sciences are easier to justify in terms of economic factors than the ‘soft’ sciences in some ways, not the least of which because only one of those two is supposed to be real science in the minds of many. I think that there appears to be a disciplinary competition, and that the social sciences is responding by falsifying and or attempting to replicate the hard science’s style of rigor.
I’m personally fond of those ‘cross-overs’ (especially cognitive mapping with behavioral design of experiments, as well as the newish complexity science take on human behavior which is popular in comp sci), but I agree that it should benefit from more rigor, and the willingness to accept falsification, rather than from the increased influence of qualitative and liberal arts methodologies.
There’s nothing wrong with frequency analysis or lexical mapping of concepts, but that competition between disciplines appears to be edging out the necessary processes in science like valuing the information which we get from dead ends, in addition to the experiments which succeed.
Pierce Butler: Results which are to the larger side of p = .05 are ‘below’ the necessary threshold for publication, despite being larger than p = .05 in value. Think of these values as being relative to that center line.
bryanpesta:
Significance is a meaningless decision and should be abandoned. At a minimum, the exact p-value should be reported, since, all else equal, the smaller the p-value, the greater the evidence against the null hypothesis. As I said above, p-values near .05 generally provide little to no evidence against the null hypothesis. Very small p-values that don’t result from very large studies, on the other hand, suggest strong evidence against the null (and there is absolutely nothing wrong with labeling those results with a phrase like “highly statistically significant”).
@ #32, #33:
I was always taught (my background is ecology and genetics, and to a lesser extent chemistry) to write along the lines of: “Treatment A increased parameter X by Y% compared to control (n = 15, p = 0.003), whereas Treatment B did not have an effect (n = 15, p = 0.134).
One of my profs was death on saying “…increased by 30%, but this effect was not significant.” His mantra was that if there was no difference, than you don’t report a difference, just the p value that led you to say there was no difference, and anytime you mentioned a difference or comparison, you HAD to mention the sample size, exact p value (or p < 0.0001) and usually the test statistic.
… I might have just broken my personal best for a run-on sentence.
Kind of nitpick-y but this isn’t strictly true. Often we will define different thresholds of significance and categorize potential findings by these thresholds. For example, when doing large-scale genotyping or resequencing-based association studies, we define different levels of significance…genome-wide significant, exome-wide significant, genome-wide suggestive, etc.
See this paper for a good discussion of this issue.
What jt512 said @31!
I kind of was rolling around in my head an idea for a journal for nothing but failed experiments. It came up after hearing about some poor grad student who had spent 18+ months finding out that his research was a dead end. Seems to me, knowing what is not true is as important as something that might be true 95% of the time.
@#40:
http://www.jnr-eeb.org/index.php/jnr
Kantalope, such journals exists in several fields. Google “journal of negative results.”
Jay
DaveH: OOooooo! Shiny!
#16:
Thanks for the offer. P values are indeed a daft way to measure research. Give me a proper probability any day. Relying on p values wastes information, as I describe here.
And yes, its a pity that PZ committed the base-rate fallacy in his second sentence of this post, and Lawrence Krauss (among many others) made the same error when describing the recent results on the Higgs boson. I can’t help feeling that its an error that contributes a lot to the popularity p values. Maybe if people were more conscious of the meaning of this number, they would feel more inclined to calculate something more relevant to the questions they want answered.
In physics, we almost never considered a p-value of 0.05 to be significant. The general perception of results with that level of significance was, “Maybe there’s something here, but there’s a pretty good chance it’s just an anomaly.” Within cosmology, the typical value for where people would start to get excited about a result would vary somewhat, but typically lay between somewhere around three sigma (p=0.003) and four sigma (p=0.0006).
One main reason is that when you start going out into the tails of the distribution, most statistical distributions, for various reasons, are no longer very Gaussian-distributed, so that what you think might be a highly-significant value might not actually be all that significant. Furthermore, failing to account for even relatively small biases can easily turn a three-sigma confidence (p=0.003) into a two-sigma confidence, perhaps even lower. So the desire within physics is to completely hammer the statistics so that there is no doubt that we’re in the regime where it’s highly unlikely that the result is just due to some experimental error.
It saddens me that so many results in other fields are published and considered reliable before being put through much more rigorous checks.
#37
Maybe we should abandon significance testing, but that’s irrelevant to how significance testing is now done. It’s a binary decision. Saying things like “marginally” or “highly” significant is wrong (again because it confuses p values with effect sizes). It’s not wrong like marrying your sister wrong. But, it is wrong.
Play around with this calculator:
http://www.danielsoper.com/statcalc3/calc.aspx?id=44
The default is a correlation of .40 with N = .40. It has a p value of .014.
Change the values so that r = .05 and N = 5000. The p value is now .0002.
By your logic, we should be far more confident that .05 effect is real?
#39
I sorta agree in that we can set alpha at any level we want. It sometimes makes sense to set it > .05 (does this drug cure cancer?). Other times it makes sense to set it < .05 (controversial research). Once it's set, though, the decision is binary.
Again, putting adjectives on p-values is technically never correct. I'd say ask Fisher, but he's dead.
@Jason Dick:
It is a case of noise in the data. Biology is much messier than chemistry or physics, mainly because there are so many sources of noise. The questions asked are also very different. In quantum physics, you are looking for tiny distinctions that give you clues in to fundemental properties. In biology, we are often asking not whether or not a process exists, but whether or not it has any sort of significant effect. A technique along this line is power analysis, which can basically be summed up as “if we missed something, how big COULD it have been, tops?”. If the answer is sufficently small, then it doesn’t matter, biologically, since any effect will be swamped by other processes.
There are cases in experimental biology where more statistical rigour might be in order, but then you run into things such as animal use. Why would I put another 20 rats through the experiment just to drop that p-value a couple points? To do so when I already am pretty sure about the answer would be unethical.
Jason Dick: I’ve always found that to be mildly to fairly hilarious when looking at distributions of populations. The assumption of normality which governs interpretation (what gets to be the threshold for significance in the social sciences) is necessary for the most common modeling, like the Least Squares methods, but somewhat ludicrous in practice.
The social science lectures I’ve had so far allow for essentially ‘eyeballing’ the population data to decide if it fits the criteria for normal. (And yes, I know there are formal test for that sort of thing.)
I mean, really, can anyone name a population which, without tossing outliers, is actually that perfect bell curve? And I say this as someone who is quite enamored of the Law of Large Numbers.
It isn’t as if many social sciences studies meet the active criteria for large enough numbers to assume normality, though re-sampling can give us some sense of the distribution.
I’d be surprised if many people using the P test had even a basic understanding of statistics. I suspect most use a small set of formulae in a very rigid fashion and don’t even understand how they can test the validity of their statistical result. In my own line of work (in which the experimental conditions can be controlled much better than in the case of many biological or sociological experiments) the P=0.05 would be unacceptable. In fact it’s generally so easy to get that P=0.05 that I always thought of the “P-test” as something which was made up so that students can do a handful of experiments and pretend that they’ve got data to form a valid conclusion.
bryanpesta:
It’s not a binary decision. It’s not even a decision. What is the point of making a distinction between a statistically significant result and a non-statistically significant result. Just because a result is statistically significant doesn’t mean it’s true. In fact, it doesn’t mean anything.
No it doesn’t confuse p-values with effect sizes. Modifiers like “marginally” or “highly” significant refer only to the size of the p-value.
No. First of all, I said, “[A]ll else equal, the smaller the p-value, the greater the evidence against the null hypothesis.” The first thing you have to keep equal is the sample size, which you increased.
Furthermore, I said, “Very small p-values that don’t result from very large studies, on the other hand, suggest strong evidence against the null.” And what did you go and do, but create a very small p-value by using a very large sample size.
I don’t really need to play around with that silly online calculator you linked to; however, you could learn a lot by playing around with this one. In particular, note what happens to the Bayes factor, which is the relative strength of the evidence in favor of the null vs the alternative hypothesis, when you hold the sample size constant and increase the value of the t statistic (which is equivalent to reducing the p-value).
Bryanpesta:
Fisher would have had no problem putting adjectives on p-values, since in his formulation of significance testing he stressed that the magnitude of the p-value was an indication of the strength of the evidence against the null hypothesis.
Now if you could ask Neyman and Pearson, they might agree with you, but they stressed the importance of carefully selecting the significance and power level of a test based on the relative costs of Type I and Type II errors. If you were to design an experiment in that manner, then it would be appropriate to treat significance as black and white. But that practice has all but been abandoned in favor of adopting conventional, meaningless significance levels.
Well, yes that’s awful, but I see a good thing here too:
I see that the scientific paradigm means we can examine and criticise our own methods and improve them, and that’s what I hope to see here. It seems to me that Masicampo and Lalande have asked the right (hard) questions.
I like the idea of Prep though, it would make things a little more transparent and less arbitrary.
jt512:
I also foresaw that at some point the Bayes factor would be introduced. Although I did not know it was you, I held a very non-uniform prior.
JT512
I don’t disagree with what you said in 50, but I’m talking about using the method and you’re talking about problems with the method. Also you are right on Fisher versus Neyman, and I did miss your “all else being equal” qualifier.
I cannot find the PDF version of this article online, but it is the basis for my claims:
http://psycnet.apa.org/index.cfm?fa=buy.optionToBuy&id=1989-31713-001
…why doesn’t this surprise me…
First question: how is this even DIFFERENT?
Second question: how do you argue that the former is not an adequate description of the latter in writing for a lay audience?
The comments are an excellent example of the difficulty of carrying out statistical analyses The Right Way.
Statisticians are just like tattooists: at any one time, there are only a handful of really good practitioners of each of these admirable arts, and a horde of also-rans. That latter category includes me and you, beloved reader.
Erm, no? .04 means that there’s a 1/25 chance of a false positive, of observing an effect when there really isn’t one, while .00001 means that that chance is only 1/100,000. When you test for 100 different randomly selected variables*, you expect around 5 false positives at a threshold of p<.05, but you're still very unlikely to find even one at .00001.
________
*Which, of course, isn't something you should be doing in the first place, in most circumstances.
p < .05 is arbitrary. You can have a sample size of 3 and an effect size of .90 won’t be significant (lost in the wilds of Minneapolis this week so don’t have my p values table on me). At the same time with 5000 subject even the most trivial of effect sizes will be significant at .05. Rather it would be better to look at the magnitude of the effect, the statistical power and the confidence interval. Just relying on p < .05 is essentially meaningless.
^ couldn’t get the quoting to work in previous post. The last 2 sentences are mine.
Also Confidence Intervals are as arbitrary as p-values as the standard error is used in calculating the width of the CI.
@Antiochus#15: On top of that we need to consider the sample population. Most studies don’t get enough funds to have a large subject population, so results of P = 0.05 should be more common than 0.01 or less. We could always turn around the plot above and say “hey, look at all those suspect 0.01 claims”. Then of course there’s the fact that the plot shown has too few points to make any reasonable claim of undue bias.
Azkyroth #56:
The first statement (the incorrect one) is the probability that the null hypothesis is true, given the data. Saying that your results “can be accounted for by accident” is the same as saying that the null hypothesis is true.
The second statement (the correct one) is (almost) the converse: the probability of the data (or more extreme data), given that the null hypothesis is true.
So, the p-value does not tell you the probability that the null hypothesis is false (called the posterior probability). The p-value can’t possibly do that because it is based on the assumption that the null hypothesis is true. For any given p-value, the probability that the null hypothesis is false can be anything from 0 to 1, depending on the plausibility (called the prior probability) of the alternative hypothesis.
Even a very small p-value will not be convincing evidence against the null hypothesis (or, equivalently, for the alternative hypothesis) if the plausibility of the alternative hypothesis is low. For example, I’d put the plausibility of the hypothesis that ESP exists at about 1 chance in 10 billion. So even if a study were fairly conducted and the resulting p-value were .000001, the study would not provide sufficient evidence to convince an appropriately skeptical reader. In contrast, if the plausibility of the hypothesis were high, say 50–50, (eg, Excedrin works better than Bayer aspirin to relieve headaches), a much more modest p-value, say .01, might be persuasive.
Because the first statement is completely wrong and is a common and serious misinterpretation of p-values among both scientists and non-scientists. The p-value does not and cannot tell you the probability that your hypothesis is true. In fact, oddly enough, under the reigning statistical paradigm (frequentist statistics), the probability that a hypothesis is true is not even recognized as a valid concept.
Oops … I didn’t quite get that right in #63. Looking at the plot again I realized that the authors must have done some binning. Looking at the original article, they do have a good sample size. I’ll have to read the article to see how they accounted for the effect of sample sizes though.
#64
I don’t think PZ’s “accident” comment was all that inaccurate.
Doesn’t rejecting the null when it’s true assume some type of fluke was present in the data?
“Saying that your results ‘can be accounted for by accident’ is the same as saying that the null hypothesis is true.” If we change the last bit to “…the null cannot be rejected” are you ok with the statement?
***
I don’t disagree with most of the recent comments. In my experience, when someone says “highly significant” they mean “large effect”. Seems like everyone here agrees that this is wrong.
I see some above use “highly significant” to mean “very likely the null is false”. This is correct, but I wonder whether most researchers use this interpretation of “highly significant”.
Whenever I see these two words, it seems like the researchers are implying the effect is therefore “real” / “important” / “large”. I still submit this is wrong for reasons discussed above (confusing p values with effect sizes).
Side note: I bet the Bayes people are right– their technique is better. I still argue, who cares. The whole debate seems based on the idea that the results of a single study can be compelling. This ignores the critical role that replication plays in scientific inference. And, I can’t imagine that effects exist (i.e., have been replicated) but only when using significance testing and not Bayesian stuff. Does anyone know of a well-replicated effect (using null hypothesis testing) that doesn’t exist when going Bayesian?
bryanpesta:I cannot find the PDF version of this article online, but it is the basis for my claims [that adjectives should not to describe degrees of significance]:
http://psycnet.apa.org/index.cfm?fa=buy.optionToBuy&id=1989-31713-001
The authors seem to think that researchers who use terms like “highly significant” when p-values are small often believe that small p-values mean large effects sizes, and they cite as evidence an informal perusal of the literature. That confusion might have been true in experimental psychology in 1989 when that article was written, but I think today, the difference between a p-value and an effect size is widely understood, and to the best of my recollection, I do not recall seeing a recent experimental psych paper that reported p-values but not effect sizes.
However, even if such confusion were still common, that does not mean that there is anything methodologically wrong with using a phrase (like “highly significant”) to communicate that a p-value is small. For a given sample size, a small p-value is stronger evidence against the null than a larger one, so I see no reason not to draw attention to that fact in a paper.
Maybe an artefact of people rounding p-values to different numbers of significant digits?
@emilkarlsson – THANK YOU for picking that nit! It bothered me as well.
Even given that some results aren’t published if p > 0.05 (and thank you, @larrylyons for pointing out the true nature of the values) this distribution does seem non-intuitive.
It’s ironic that in their article about miss use of significance testing that the authors use “marginal significance” (p =.08) knowing full well that .08 is not significant.
I also see this as potentially driven more by publication bias than fudging. I had previously thought that the number of published studies in education research that use small sample sizes and talk about differences that are not statistically significant was a bug, but it would appear to be a feature if it means negative results in larger followup trials are more likely to be published.
I would think meta-analyses would take care of this sort of ‘fudging’ in cases that really matter — medicine, say.
For anything other field/effect, I think comments here have already suggested that the effect-size matters more than the p-value.
*shrug*
Could be.
what is the p value on this study of p values? my first impression is that the bump in the data is just a statistical variation. however, all the other points lie pretty close to the theoretical curve. plus they used about 3200 articles, which seems like a big enough N to reduce statistical fluctuations in the data.
i would like to see the study reproduced with more than one year of articles, say 10 years worth.
it certainly *seems* like it may be a real bump, but i am not convinced yet.
p.s. is that plot made with Excel? what serious researcher uses Excel? meh, at least they have a best fit curve and didn’t use the frackin’ scatter plot with the connect-the-dots fit.
one more thing: where are the error bars?
I’m tempted to quote “the closer you get to humans, the worse the science gets”, but I second the call for a metanalysis of results in particle physics and the like that was suggested on the ScienceBlogs version of this thread: does particle physics have such a spike of results that are just beyond 5 σ (corresponding, incidentally, to p = 0.0000005733)?
In other words, if you throw 100 statistical tests at the same question, on average 5 of them will find p < 0.05. Corrections need to be done for multiple statistical tests of the same hypothesis; such corrections exist, as mentioned above, but some authors and some reviewers may not know that.
Do you know a case where the null hypothesis is not “it’s all random, there’s no cause or effect going on, nothing to see here, move along”?
Yep. If a process is theoretically possible, it most likely happens in nature, but it may still be laughably negligible.
Lots.
If nothing else, Excel comes as part of Office, and you need Word anyway.
Coor Singh:
Shenanigans used to attain statistical significance inflate the effect size, and will thus bias the aggregate effect size in a meta-analysis. Consider an investigator who runs 20 pilot studies on a single hypothesis, each with a different set of test questions. All of the studies had non-significant results, but one was close, with a p-value of .055. These are exactly the type of results you would expect to see if your null hypothesis was true, but the investigator interprets it differently, thinking that the test questions in the close-to-significant study are more sensitive to the hypothesized phenomenon. So he makes that study the main study and tests an additional 20 subjects. The results of the 40-subject test are significant, with p=.45.
Getting one significant result out of 20 tests of the same hypothesis is evidence that the hypothesis is false, so the true effect size is zero. If a meta-analysis had access to all 20 studies it would correctly conclude that, but future meta-analyses using only published reports will not. If the true effect size is 0, then all published studies will have inflated effect sizes, and so will the result of the meta-analysis.
But if significance chasing is prevalent in the field, the effect size in the literature will be exaggerated.
bryanpesta #64:<I don’t think PZ’s “accident” comment was all that inaccurate.
Doesn’t rejecting the null when it’s true assume some type of fluke was present in the data?
The probability that your results are due to “accident” (ie, chance) is the probability that your results are due to the null hypothesis being true. Therefore, your results are due to chance if and only if the null hypothesis is true. Therefore, the probability that your results are due to chance is the probability that the null hypothesis is true. This is a probability about a hypothesis, and therefore a probability that doesn’t exist in frequentist statistics. Since the p-value is a frequentist statistic, PZ’s definition cannot be correct. Furthermore, since we have the data, PZ’s definition is a posterior probability. In fact, it’s the posterior probability of the null hypothesis given the data, P(H₀|D). It’s exactly what we calculate in a Bayesian analysis, but p-values aren’t Bayesian.
The definition of a p-value is close to the converse of P(H₀|D). It is the probability of the data, or more extreme data, if the null hypothesis is true. It is a number like P(D|H₀). It’s a probability about the data, rather than the hypothesis. So PZ’s definition is fundamentally wrong; he basically transposed the conditional.
No, as explained above, that’s not the issue.
[I blew the blockquotes above. Here is a properly formatted version of my comment.]
bryanpesta #64:
The probability that your results are due to “accident” (ie, chance) is the probability that your results are due to the null hypothesis being true. Therefore, your results are due to chance if and only if the null hypothesis is true. Therefore, the probability that your results are due to chance is the probability that the null hypothesis is true. This is a probability about a hypothesis, and therefore a probability that doesn’t exist in frequentist statistics. Since the p-value is a frequentist statistic, PZ’s definition cannot be correct. Furthermore, since we have the data, PZ’s definition is a posterior probability. In fact, it’s the posterior probability of the null hypothesis given the data, P(H₀|D). It’s exactly what we calculate in a Bayesian analysis, but p-values aren’t Bayesian.
The definition of a p-value is close to the converse of P(H₀|D). It is the probability of the data, or more extreme data, if the null hypothesis is true. It is a number like P(D|H₀). It’s a probability about the data, rather than the hypothesis. So PZ’s definition is fundamentally wrong; he basically transposed the conditional.
No, as explained above, that’s not the issue.
If borderline (ie p=0.051) results are being fudged into 0.049 results, you would expect a similarly sized deficit on the high side of the 0.05 line. There is a small deficit, but it seems to be in line with the noise on the rest of the plot, and not nearly the size of the excess below 0.05.
I’m not sure where to go with that other than it doesn’t fit into the fudging borderline results theory.
If it isn’t publication standards, it’ll be something else, perhaps just wishful thinking. You can’t start out recognizing that the metric is arbitrary and end up worrying about whether the metric is actually being met. That’s just being prissy.
Reminds me when I had a problem with my experiments some years ago. Model biased fit and unbiased fit of the model to the data had a gap of 6.5%. Anything higher than 5% between both is considered biased by the model. I asked a colleague about suggestions. She said I need to find a “creative way of publishing it”. I looked stupid for a while and went back to the computer. Spent ~4 month on improving the model which resulted in a spread of 2.5% between the free and the restrained data. Nothing creative about that. Just a lot of work.
@80: Maybe people are fudging results all across the board? I don’t know.
Maybe someone should do a study to find the possible causes.
g #80:
I think what you’ve termed the “borderline” is too narrow. The p-values in the graph only go up to .10, and the range from .05 to .10 is often thought of as bordering on significance. Seeing a result with a p-value in this range could certainly motivate an incautious researcher to take a few more samples to hopefully reduce the p-value to the official level of significance or to look for significance in ad hoc subgroups.
vaiyt #83:
That is certainly plausible, too. If the null hypothesis is true, all p-values between 0 and 1 and are equally likely, and it only takes 20 tries on average to get 1 p-value below .05. Bem (2011) was almost certainly studying a true null hypothesis (ESP), and he apparently had no trouble publishing the results of 10 statistically significant experiments—suggesting that it is apparently not that difficult to file-drawer approximately 190 non-significant results whose p-values would have randomly ranged from .05 to 1.
Well, it seems that a very common misconception out there is that p < 0.05 = less than 5% probability the null hypothesis is true = over 95% probability the test hypothesis is true, given the data.
But this applies only if the null and test hypotheses are the only two hypotheses out there that can explain the data – and that in reality is never true.
…and if the null hypothesis is true, but your samples differ, it has to be due to sampling error, i.e. ‘accident’. yeesh.
I use Excel. A lot. Not for published figures (SigmaPlot) or the kind of statistics I do (Systat), but for data manipulation and visualization; sometimes even simple stats. Works fine if you know what’s what. But definitely designed for busy-ness people, not scientists.
Amphiox:
You have correctly stated the common misconception, but wrongly stated the reason for it. It has nothing to do with the number of alternative hypotheses there are (which are usually infinite in practice anyway). You’ve pulled a “PZ” (see my #79, but be kind and ignore the redundant sentences)” and transposed the conditional. The p-value is the probability of the data (or more extreme data), given that the null hypothesis is true, roughly P(D|H₀). The probability that the null hypothesis is true, given the data, P(H₀|D), is the posterior probability of the null hypothesis, and must be calculated by using Bayes’ Theorem.
@jt512
That was my first reaction, as well.
I am almost completely certain that that is not what it says. It might be what the writer thinks, of course.
If the results can be accounted for by accident, then what is the accident in question? I can see no candidate other than the results. That is, this says almost exactly what your version says (it does not explicitly mention more extreme results): “probability it can be accounted for by accident” is “probability of obtaining the results if the null hypothesis is true”. And it does not talk about the probability of the null hypothesis. I really cannot see how you can justify your reading.
khms:
I think it is more likely the other way around: that PZ knows what a p-value is, but in trying to communicate it to a lay audience, he oversimplified it.
That makes no sense. If the results can be accounted for by accident, and the accident is the results, then you are saying that the results can be accounted for by the results, which is nonsensical.
The probability that the results can be accounted for “by accident” means the probability that the results can be accounted for by random chance. Let’s say we conduct an experiment to measure some quantity—call it Z. Our null hypothesis is that the true value of Z is 0, and our alternative hypothesis is that the true value of Z is not 0. We conduct our experiment, and get the result Z=2.0, p-value .045, which is barely statistically significant. Is the probability that our result can be accounted for by random chance .045? Let’s see.
The phrase “our result can be accounted for by random chance” is shorthand for saying that our result was not due to a real effect, but merely differed from 0 by random chance; that is, the alternative hypothesis is false, and the null hypothesis is true. It follows that in order for us to have gotten our result (Z=2.0) by chance, two things have to be true: (1) the null hypothesis must be true and (2) we had to have gotten the result Z=2.0. Therefore, the probability that we got our result by chance must be a function of (#1) the probability that the null hypothesis is true and (#2) the probability of getting Z=2.0, given that the null hypothesis is true. But we have already agreed that (#2) itself is the definition of the p-value (except for the omitted “more extreme than” clause), and (#2) does not depend on (#1). Therefore, the p-value cannot be the probability that the result is due to chance.
In fact, the probability that the result is due to chance is precisely the Bayesian posterior probability of the null hypothesis, and must be computed by using Bayes’ Theorem from the relative likelihood of the result (which can sometimes be computed from the p-value) and the prior probability of the null hypothesis.
To answer the question originally posed—is the probability that our results occurred by chance .045?—we have no idea, because do not know (or we have not specified) the prior probability of the null hypothesis.