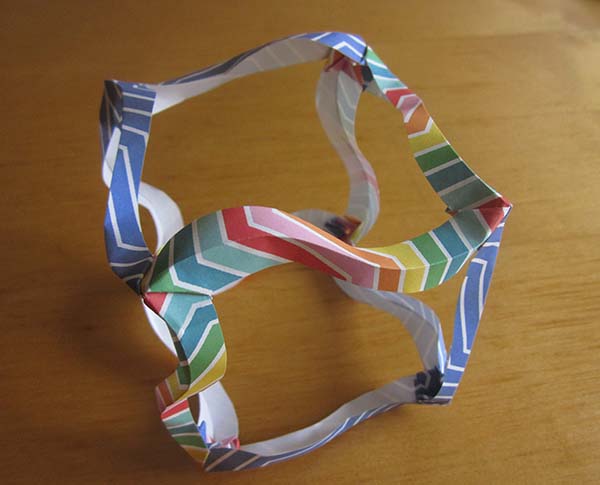Waterbomb Curve, designed by me
This is a variant on the so-called waterbomb tessellation (a photo of which you can find somewhere in my blog archives).
A neat thing about the waterbomb tessellation is that it naturally curves into a sphere-like shape. The tensions in the paper cause the tessellation to have an overall positive Gauss curvature,* like the surface of a sphere. So I was thinking about how cool it would be to patch together multiple waterbomb tessellations, some concave up, and some concave down. This here is the result.
*My understanding of differential geometry tells me that what determines the shape is mean curvature rather than Gauss curvature, but if you don’t know what that is then never you mind. ETA: On second thought I’m not sure this makes a lick of sense.