Remember when I drew 98 cubes?  Well, this time I drew 164 dodecahedra.  I created an infographic-style diagram of dodecahedron/icosahedron symmetries.

This image is very large, so I’m putting a small version below, and you can get the full size on my Flickr page.

This image is under CC BY-NC-SA 2.0. Click for the full size (hosted on Flickr).

Understanding the diagram

I already had some explanation back when I made a diagram of every cube symmetry, but there’s value in repeating myself with different words.

A symmetry group is a set of transformations (i.e. rotations and reflections) that leave an object unchanged.  For example, the letter “V” is symmetric because it’s identical to its reflection.  So “V” has a symmetry group with two transformations: the identity transformation, and a reflection transformation.

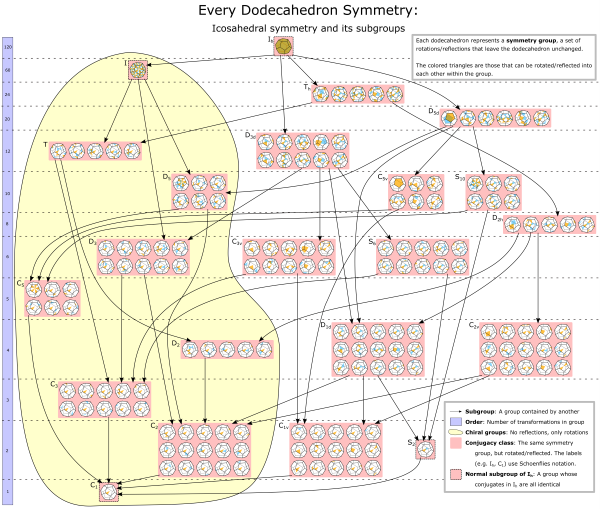
Symmetry groups can get much more complicated, with the dodecahedron having 120 symmetries.

Symmetries obey certain rules.  For example, if rotation X is a symmetry, and reflection Y is a symmetry, then so is the transformation consisting of rotation X followed by reflection Y.  The properties of symmetry groups are studied in group theory, a branch of mathematics.  Symmetry groups aren’t the only type of group–“group” is a generalization.  However, here we’re only concerned with symmetry groups.

In this diagram, I represent a bunch of symmetry groups (164 symmetry groups in total).  Each symmetry group is represented by a dodecahedron, with a number of triangles on its surface colored in.  Orange or blue doesn’t matter, it’s just to distinguish triangles on the front (orange) vs the back (blue).  Each symmetry group consists of the transformations that will rotate/reflect the colored triangles into one another.  (In mathematical terms, the set of colored triangles is an “orbit”.)

The symmetry groups have a sort of hierarchy.  Some symmetry groups contain other symmetry groups.  For example, I_h is the largest symmetry group, containing 120 symmetries. I is a smaller symmetry containing 60 symmetries.  All 60 symmetries in I are also contained in I_h. Therefore, I is a “subgroup” of I_h. This is indicated by an arrow from I_h to I.

Many of the symmetry groups are placed together in pink boxes.  These are “conjugacy classes”.  For example, consider the symmetry group consisting of the identity transformation and a single reflection.  That’s well and good, but which reflection?  There are many different reflections to choose from, and so this description applies to 15 distinct symmetry groups.  We say that the 15 symmetry groups are conjugates of one another, and that the set of 15 groups is a conjugacy class (C_1v in the diagram).

Comparing the cube and dodecahedron

After making the diagram of every cube symmetry, I wanted to make another for every dodecahedron symmetry, but it took me a while.  That’s because there are a lot more dodecahedron symmetries.  On the other hand, in some ways the dodecahedron is actually simpler, having fewer arrows and fewer conjugacy classes.  Here are the totals:

Cube:

• 98 symmetry groups
• 25 conjugacy classes under all rotations/reflections
• 33 conjugacy classes under cubic symmetry
• 80 arrows

Dodecahedron:

• 164 symmetry groups
• 22 conjugacy classes under all rotations/reflections
• 22 conjugacy classes under dodecahedral symmetry
• 45 arrows

The cube also had a complication that there was a distinction between conjugacy classes under all rotations/reflections, and conjugacy classes under cubic symmetry.  This is tricky to explain without getting into details about how to define a conjugate.  For the dodecahedron, I don’t need to make the distinction.

Other neat facts

In group theory the symmetry group of the dodecahedron–if you exclude reflections–is what’s called a “simple group”.  A “simple group” is analogous to a prime number.  A prime number has only two divisors: itself, and one.  A simple group has only two normal subgroups: itself, and the trivial group.  A normal subgroup is a subgroup with no distinct conjugates.

Why does the title go back and forth between dodecahedra and icosahedra?  The canonical name of the symmetry group is the icosahedral symmetry group.  However, it’s identical to the symmetries of the dodecahedron, and it’s much easier to visually represent a dodecahedron.  The problem with visually representing a polyhedron in a flat diagram is that I have to make sure that none of the faces are parallel to the line of sight.  The icosahedron has 20 faces, while the dodecahedron only has 12, so the dodecahedron is easier to represent.

(In my previous diagram, I drew cubes for the same reason.  The canonical name is the octahedral symmetry group, but it’s identical to the symmetries of the cube.  A cube is easier to represent because it has fewer faces than an octahedron.)

Previously, I stated there were 174 subgroups of the icosahedral symmetry group, but I had to revise this number down to 164.  That was based on an error on Wikipedia that I hadn’t noticed until I started diagramming them out.  That’s part of the reason why I wanted to draw this diagram, because I kept on referring to the Wikipedia article, but it’s hard to read and contains several errors.