[Part 3]
The programs comprising the human mind were designed by natural selection to solve the adaptive problems regularly faced by our hunter-gatherer ancestors—problems such as finding a mate, cooperating with others, hunting, gathering, protecting children, navigating, avoiding predators, avoiding exploitation, and so on. Knowing this allows evolutionary psychologists to approach the study of the mind like an engineer. You start by carefully specifying an adaptive information processing problem; then you do a task analysis of that problem. A task analysis consists of identifying what properties a program would have to have to solve that problem well. This approach allows you to generate hypotheses about the structure of the programs that comprise the mind, which can then be tested.[1]
Let’s try this approach. My task will be to calculate the inverse square root of a number, a common one in computer graphics. The “inverse” part implies I’ll have to do a division at some point, and the “square root” implies either raising something to a power, finding the logarithm of the input, or invoking some sort of function that’ll return the square root. So I should expect a program which contains an inverse square root function to have something like:
float InverseSquareRoot( float x )
{
return 1.0 / sqrt(x);
}
So you could imagine my shock if I peered into a program and found this instead:
float FastInvSqrt( float x )
{
long i;
float x2, y;
x2 = x * 0.5;
i = * ( long * ) &x;
i = 0x5f3759df - ( i >> 1 );
y = * ( float * ) &i;
y = y * ( 1.5 - ( x2 * y * y ) );
return y;
}
Something like that snippet was in Quake III’s software renderer. It uses one step of Newton’s Method to find the zero of an equation derived from the input value, seeded by a guess that takes advantage of the structure of floating point numbers. It also breaks every one of the predictions my analysis made, not even including a division.
The task analysis failed for a simple reason: nearly every problem has more than one approach to it. If we’re not aware of every alternative, our analysis can’t take all of them into account and we’ll probably be led astray. We’d expect convolutions to be slow for large kernels unless we were aware of the Fourier transform, we’d think it was impossible to keep concurrent operations from mucking up memory unless we knew we had hardware-level atomic operations, and if we thought of sorting purely in terms of comparing one value to another we’d miss out on the fastest sorting algorithm out there, Radix sort.
Radix sort doesn’t get implemented very often because it either requires a tonne of memory, or the overhead of doing a census makes it useless on small lists. To put that more generally, the context of execution matters more than the requirements of the task during implementation. The simplistic approach of Tooby and Cosmides does not take that into account.
We can throw them a lifeline, mind you. I formed a hypothesis about computing inverse square roots, refuted it, and now I’m wiser for it. Isn’t that still a net win for the process? Notice a key difference, though: we only became wiser because we could look at the source code. If FastInvSqrt() was instead a black box, the only way I could refute my analysis would be to propose the exact way the algorithm worked and then demonstrated it consistently predicted the outputs much better. If I didn’t know the techniques used in FastInvSqrt() were possible, I’d never be able to refute it.
On the contrary, I might falsely conclude I was right. After all, the outputs of my analysis and FastInvSqrt() are very similar, so I could easily wave away the differences as due to a buggy square root function or a flaw in the division routine. This is especially dangerous with evolutionary algorithms, as Dr. Adrian Thompson figured out in an earlier installment, because the odds of us knowing every possible trick are slim.
In sum, this analysis method is primed to generate smug over-confidence in your theories.
Each organ in the body evolved to serve a function: The intestines digest, the heart pumps blood, and the liver detoxifies poisons. The brain’s evolved function is to extract information from the environment and use that information to generate behavior and regulate physiology. Hence, the brain is not just like a computer. It is a computer—that is, a physical system that was designed to process information. Its programs were designed not by an engineer, but by natural selection, a causal process that retains and discards design features based on how well they solved adaptive problems in past environments.[1]
And is my appendix’s function to randomly attempt to kill me? The only people I’ve seen push this biological teleology are creationists who propose an intelligent designer. Few people well studied in biology would buy this line.
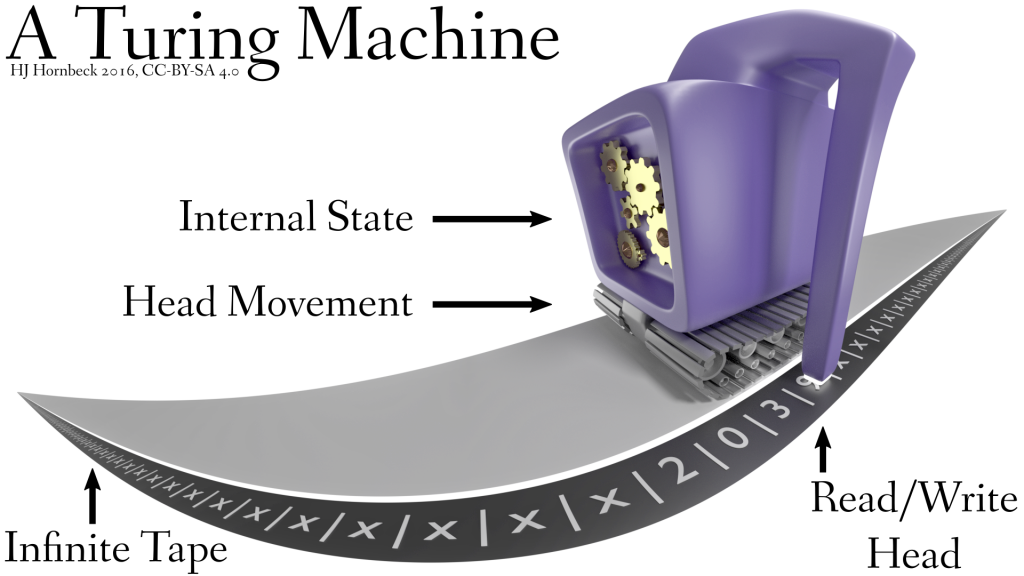
But getting back to my field, notice the odd dichotomy at play here: our brains are super-sophisticated computational devices, but not sophisticated enough to re-program themselves on-the-fly. Yet even the most primitive computers we’ve developed can modify the code they’re running, as they’re running it. Why isn’t that an option? Why can’t we be as much of a blank slate as forty-year old computer chips?
It’s tempting to declare that we’re more primitive than they are, computationally, but there’s a fundamental problem here: algorithms are algorithms are algorithms. If you can compute, you’re a Turing machine of some sort. There is no such thing as a “primitive” computer, at best you could argue some computers have more limitations imposed on them than others.
Human beings can compute, as anyone who’s taken a math course can attest. Ergo, we must be something like a Turing machine. Is it possible that our computation is split up into programs, which themselves change only slowly? Sure, but that’s an extra limitation imposed on our computability. It should not be assumed a-priori.
[Part 5]
[1] Tooby, John, and Leda Cosmides. “Conceptual Foundations of Evolutionary Psychology.” The Handbook of Evolutionary Psychology (2005): 5-67.