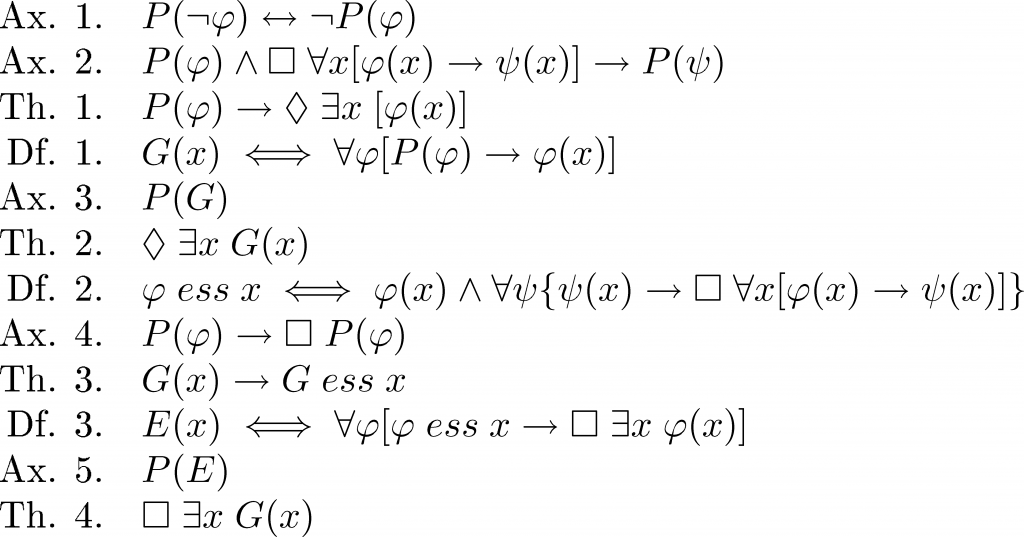Proof from Logical Necessity, or the Ontological Proof
I’m going to need your help with this one. Relax and get comfortable.
Now, I’d like you to imagine the most perfect being. One that embodies all the qualities you’d like to be in a conscious entity. A perfectly-balanced sense of judgement, say, or a deep pool of empathy and caring, or a graceful ability to forgive and move on, or a wisdom well beyond its years. Picture an entity that manages all that, better than anything that has or will exist.
It’s a lovely thought, isn’t it? Don’t you wish such an entity existed?
I bet you’d agree that it’s better to exist than not exist, right? A being that has all those traits would be more perfect if it existed than a similar being that did not. And yet, you had no problems picturing that perfect entity, didn’t you? How could you have pictured perfection without including every portion of that perfection, including the ability to exist?
The ease of picturing perfection, therefore, must mean that perfection exists. And since a god matches that perfection to a tee, that must mean the gods exist.
No Really, It’s Quite Popular With Some People
Most of you are scratching your heads right now. “Really? That’s a proof?”
It is, and it’s been a favourite of philosophers for some time. Despite the “-logical” suffix, most scholars do not think this proof was dreamed up by a Greek. I’m not so sure; while it’s true that I can’t find a single example within their works, you’ll note that it bears a strong resemblance to the Cosmological proof, which was quite popular with them. Indeed, my description above is almost identical to variation of Cosmological. Instead of stepping up one degree of perfection, however, I stepped sideways and invoke the property of “existence.” Thus Ontological proofs do not “step outside” the universe, and are immune to that particular counter-argument.
There’s a better argument for this proof’s origins, that a fan of Greek learning came up with this twist. Avicenna[22] was a Persian philosopher who lived roughly 1.5 millennia after the Greeks, but was one of the few people in the world to have access to their written texts. He claims to have memorized the entire Qur’an by age ten and outsmarted his teachers by age fourteen, which sounds unlikely until you start cataloguing his accomplishments. Avicenna pioneered the use of clinical trials, knew the heart worked as a valve, discovered Newton’s first law of motion, reasoned that light had a finite speed, came pretty close to inventing Germ Theory, was the first psychologist, published a book of medicine that was used for 600 years in Europe, and during a moment of boredom invented the refrigerated coil and scented oils. As if to further rub it in, half of his surviving work is
written in verse.
A lover of Aristotle, Avicenna extended the old Greek’s philosophy and applied it to Islam. I can track down several scholars, such as M. E. Marmura and Parviz Morewedge, who make it quite clear that Avicenna’s proof differed from his classical hero by focusing more on logic and existence, independent of physical reality:
It is not in any sense a proof that infers God’s existence from the observation of His handiwork. On this Avicenna is explicit. After giving one version of his proof from contingency, for example, he writes: “Reflect on how our proof for the existence and oneness of the First and His being free from attributes did not require reflection on anything except his existence itself and how it did not require any consideration of His creation and acting, even though the latter [provide] evidential proof (dalīl) for Him. This mode, however, is more reliable and noble, that is, where when we consider the state of existence, we find that existence inasmuch as it is existence bears witness to Him, while He thereafter bears witness to all that comes after Him in existence” (Ešārāt, p. 482).
(M. E. Marmura, Encyclopædia Iranica, http://www.iranica.com/articles/avicenna-iv, retrieved April 30th 2011)
Other scholars dispute Avicenna’s departure, and unfortunately I can’t track down a translated version of his Šefāʾ or Ešārāt to decide for myself.
I can track down the original texts of Anselm of Canterbury, however. His book Proslogion is universally accepted as a true proof from Logical Necessity. Anselm had a rather interesting life, most notably feuding with two kings of England and being forced into exile twice. It’s a shame the topic of this book doesn’t permit me to go into more details, because those decades of political intrigue would be easier to sort out than Anselm’s writing:
In fact, it [God] so undoubtedly exists that it cannot be thought of as not existing. For one can think there exists something that cannot be thought of as not existing, and that would be greater than something which can be thought of as not existing. For if that greater than which cannot be thought can be thought of as not existing, then that greater than which cannot be thought is not that greater than which cannot be thought, which does not make sense. Thus that than which nothing can be thought so undoubtedly exists that it cannot even be thought of as not existing.
(Proslogion, Chapter 3: “That God Cannot be Thought Not to Exist”, as translated by David Burr)
Since I’m not a cruel person, I’ll spare you from having to parse the original and write up my own translation:
Chapter 2: That God Really Exists
1. No being is greater than God. Even a fool who would deny God recognizes this.
2. That fool has only a partial understanding, however, since he does not understand such a being to exist.
3. Consider a painter’s thoughts of his or her next masterpiece, to the finished masterpiece itself. They have a rough sketch of the painting within their minds, but since it does not physically exist they cannot fully understand that painting.
4. It follows from 3. that it is greater for any object to exist that to not exist.
5. But if point 4. is true, then it would be impossible to think of the greatest possible being unless that being existed. Otherwise, there could exist a greater being, having all the attributes you gave to your greatest being plus the attribute of existence.
Chapter 3: That God Cannot be Thought Not to Exist
6. We can think of a being that must exist, and this being must be greater than one that we cannot think of as existing.
7. By that reasoning, if that being from 4. couldn’t exist, it would be lesser than another thing in our thoughts that could exist in reality.
8. Thus, we’ve reinforced point 5: that being must exist in reality.
9. By extension of points 6 through 8, we cannot even think of this being as not existing.[23]
10. We can’t think of anything greater than God.
11. This “being” we’ve been referring to must be God, otherwise we’d contradict point 10.
12. Praise God, isn’t He wonderful, etc. etc. etc.
Philosophers fell in love with this style of proof. The possibility of finding a proof for god using nothing but logic is like finding a long-forgotten civilization without leaving the house. A number of big-names have come up with their own versions, such as Gottfried Leibniz, Kurt Gödel, and René Descartes. The Stanford Encyclopaedia of Philosophy lists five more “distilled” variations on it:
1. God is a being which has every perfection. (This is true as a matter of definition.) Existence is a perfection. Hence God exists.
2. [24]
3. It is possible that God exists. God is not a contingent being, i.e., either it is not possible that God exists, or it is necessary that God exists. Hence, it is necessary that God exists. Hence, God exists.
4. [It is analytic, necessary and a priori that][25] Each instance of the schema “The F G is F” expresses a truth. Hence the sentence “The existent perfect being is existent” expresses a truth. Hence, the existent perfect being is existent. Hence, God is existent, i.e. God exists. (The last step is justified by the observation that, as a matter of definition, if there is exactly one existent perfect being, then that being is God.)
5. The word ‘God’ has a meaning that is revealed in religious experience. The word ‘God’ has a meaning only if God exists. Hence, God exists.
6. I exist. Therefore something exists. Whenever a bunch of things exist, their mereological sum also exists. Therefore the sum of all things exists. Therefore God—the sum of all things—exists.
(http://plato.stanford.edu/entries/ontological-arguments/ , retrieved April 30th 2011)
Missing from that list is Leibniz’s Monad theory, which borrows an ancient Greek idea. A “monad” is a super-atom of sorts; they make up every substance and contain consciousness, yet cannot be changed or destroyed, only divided into infinitely small pieces. No two are alike. They’re classified by the abstract properties they’ve been granted; “Entelechies” do little more than move, “Souls” have the added ability to remember things, and “Spirits” are permitted to reason. While all modads are tied to physical bodies, Leibniz claims there’s a special monad out there that is not attached to a body, and does nothing but continually create new monads. This god monad is stopped from just cranking out “Spirits” by the laws of nature. This system cannot be improved on, according to Leibniz.
None of Leibniz’s contemporaries agreed on that point.
The sixth on that list is a close match for Descartes’ “proof” for God. The scare-quotes are because Descartes would probably object to that argument being called a proof, let alone one of his own. In general, he thought God’s existence was obvious via intuition, instead of rational arguments. As a result he never bothered to write up a formal rationale, but instead randomly scattered bits of logical argument and informal reasons throughout his work. He took full advantage of this sloppiness, by throwing out many variations and forcing his critics to comb through his entire work to clean up his “proofs.” Fortunately for me, his arguments boil down to a mix of proofs that I have or will cover in this book, so I don’t need to elaborate further.
Gödel’s proof, by comparison, is both much better and much worse. Instead of dealing with “perfections” or simplistic “attributes,” his proof works on “positive, morally aesthetic properties;” examples of these include “perfectly just,” “all-powerful,” “merciful,” and “absolutely moral.”
Out of all the Ontologicals I’ve presented, Gödel’s is easily my favourite. It’s much better than Descartes’ “proof” because it is a well-structured logical argument, presented in a formal logical system with well-defined rules. It’s also much worse, for the same reason:
That chart-junk is called “modal logic,” and is a little tough to understand without study. Would another translation help?
Assumption 1: No property in collection P will be the inverse of another property also in P.
Assumption 2: If a property is in P, and if for all objects with that property that implies the existence of some other property in every possible situation, then the collection P also contains the other property.
Theorem 1: If a property is in P, an object might exist with that property.
Definition 1: An object has the “God-like” property if, and only if, that object has every property in P.
Assumption 3: The “God-like” property is in P.
Theorem 2: At least one object might have the “God-like” property.
Definition 2: A property is an “essential property” of an object if, and only if, every property that object has must be implied by the essential property, in every possible situation.
Assumption 4: Any property in P must be within P in every situation.
Theorem 3: If an object has the “God-like” property, that property must be an essential property.
Definition 3: An object has the “Anselmian God” property if, and only if, all its essential properties imply that, in every possible situation, an object exists with that essential property.
Assumption 5: The “Anselmian God” property is in P.
Theorem 4: There must exist an object with the “God-like” property in every situation.
I think this is enough examples to begin pulling out some common threads. To begin with, Ontological proofs ignore concepts grounded in reality and instead focus on using pure logic. The only potential exception is “existence,” depending on whether or not you think ideas have an existence outside or independent of the universe. From there, they start rattling off attributes and properties of god, and through some carefully-constructed logic come to the conclusion “god exists” by proving something god-like has the attribute of “existence.”
[22] This is the Latinized version of his name; in the Middle East, he was known as Abū ʿAlī al-Ḥusayn ibn ʿAbd Allāh ibn Sīnā, which was sensibly shortened down to Ibn Sīnā.
[23] Points 6 through 9 match up with the section of Proslogion that I quoted earlier, so you can decide how accurate my attempts at translation were for yourself.
[24] The second version is the rephrasing of Anselm’s argument I quoted earlier.
[25] My best translation from philosopher-ese is “it follows from and is proven from prior knowledge that…”