cn: It’s math

When I was an experimental physicist, one of the difficulties was the sheer number of different knobs you could tune… the power of the laser, the rate of laser pulses, the angle of the laser, the material being measured, the temperature, and numerous other knobs more difficult to explain. The search space was too large, and I had to judiciously choose what things to measure.

But in some ways, it’s easier in physics. I had a lot of physics theory to inform my expectations. Suppose you’re designing a website for a personal business, there isn’t quite as much theory to tell you what design features will drive business. You might be stuck trying everything, throwing stuff at a wall until something sticks.

It turns out there’s some interesting math behind this. If you throw everything at a wall, that’s an awful lot of things. But there are ways to throw fewer things at the wall and get about the same information from your experiment.

Suppose that there are a discrete and well-defined number of things you’d like to try on your website: a photo of yourself, an intro video, comic sans font, a bright purple background, flashing text, frequent all-caps, autoplay music, and so on.* Each of these things is called a “treatment”, and there’s a version of your website that has a treatment and another version that does not have the treatment. There are seven treatments, so that’s what 2^7=128 versions of your website?

*I was recently playing Hypnospace Outlaw.

So one thing you could do, is test all 128 versions. That’s the “throw everything at the wall” strategy, but more formally it’s called a full factorial experiment. You can make a chart like the one below, which shows which treatments are applied in each of your 128 tests.

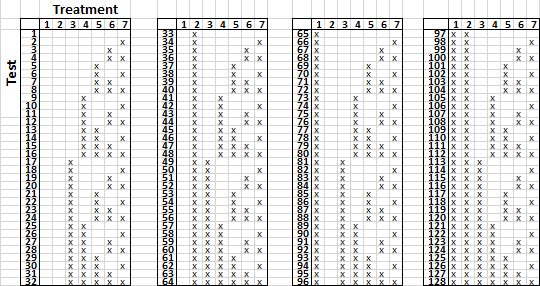
I had to make the text small to fit it all in.

Suppose that the experiment can be run on about 500 visitors. You might be concerned that each version of the website only gets about 4 visitors, N=4 is too small to draw any conclusions. But rather than thinking about it as a test of 128 websites, think of it as a test of 7 treatments. For each treatment, we have N=250 with the treatment and N=250 without the treatment. That’s enough to draw conclusions.

Full factorial experiments are fine, but maybe it’s a bit overkill. There are also practical considerations–if you can program your website to procedurally generate 128 versions that’s great, but what if you have to manually code each one individually? (One might say, then you have no business trying to run this experiment at all, but…) Could you get away with using only a fraction of every possible version of your website?

You can, of course, do it with just 8 tests. One version with no treatments, and seven versions each with a different single treatment. But this isn’t quite as good, because each treatment is only tested on one eighth of your visitors.

So there’s another method called a fractional factorial experiment, which takes a fraction of the tests from the full factorial experiment. This design also uses only 8 tests, but each treatment is applied to half of your visitors.

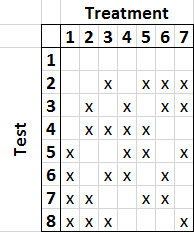
I can make a chart with big font now!

I got excited when I first saw this chart because I thought… it’s so symmetric! Each treatment is applied in exactly half of the tests. Furthermore, for any pair of treatments, they are both applied in exactly one fourth of the tests.

For those who want details, here’s how I wrote out that table. Treatments 1, 2, and 3 follow full factorial design. Then I take an XOR operation of treatments 1 and 2, and that determines whether treatment 4 is applied. I also take 1 XOR 3 (treatment 5), 2 XOR 3 (treatment 6), and 1 XOR 2 XOR 3 (treatment 7).

There is a disadvantage to this experimental design, in that it assumes that none of the treatments interact with one another. For example, maybe it turns out that purple backgrounds and flashing letters aren’t great individually, but people just love them in combination. Let’s say purple backgrounds is treatment 1, and flashing text is treatment 2. Because treatments 1, 2, and 4 are never applied together, this makes treatment 4 look worse than it really it is.

But fractional factorial design is versatile, so it can solve that problem too, if you’re willing to include more tests. Here’s an experimental design with 16 tests that doesn’t have that problem.

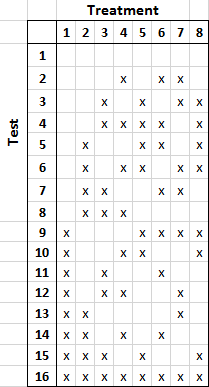
I can even fit an extra treatment into this table.

This still assumes that there aren’t any 3-treatment interactions. You can solve that problem with even more tests. And if you’re worried about 4-treatment interactions, you can add even more tests and so on.

And that’s about all I have to say about it.  I just find it really neat when combinatorics has something approaching an application like this.