A few days ago, the Nobel Prize in Physics was awarded to Haldane, Kosterlitz, and Thouless, ”for theoretical discoveries of topological phase transitions and topological phases of matter”.  Hey, I recognize two of those names!  In my field of research, superconductivity, there’s something known as the Berezinskiĭ-Kosterlitz-Thouless transition.  (Berezinskiĭ didn’t win the Nobel because he died in 1980.)

As always, the Nobel provides an article explaining the background for popular audiences.  I’m just going to talk about it briefly to give you the gist.

Berezinskiĭ, Kosterlitz, and Thouless (BKT) explained the superconducting transition in flat, 2-dimensional materials.  Below a certain temperature, the material becomes a superconductor, conducting electricity with precisely zero resistance.  Above that temperature, it behaves as a normal material.  What changes?

Superconductors have topological defects called vortices (singular form is “vortex”), which I depict below:

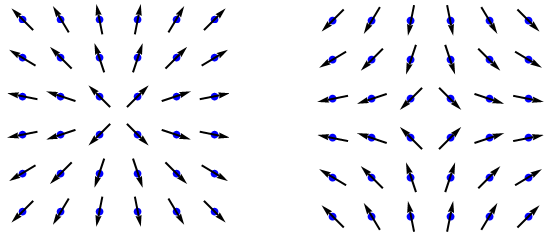
Here, each blue circle is an atomic site, and the arrow represents the “phase” of the superconductor.  The two squares above show the two kinds of vortices, the “+” vortex and “-” vortex.  These vortices behave as electrical charges, with like repelling like, and opposite charges attracting.

Another thing about these vortices: They are a loophole which might cause a superconductor to have electrical resistance.  Indeed, if vortices are allowed to roam freely through a superconductor, you might have a superconductor with nonzero resistance, hardly a proper superconductor at all.  This is what happens at the BKT transition!  Above this temperature, vortices can roam freely, leading the material to have nonzero resistance.  Below this temperature, vortices become bound, with each “+” vortex paired up with a “-” vortex.

The mathematics that describe the BKT transition are quite general, and apply to any 2-dimensional material that has some sort of “phase”.

Moving onwards, let’s talk about Haldane.  I’m afraid that I don’t understand his work as well as that of the others, but I’ll give a brief overview.

Normally, when you apply an electric field to a material, the current flows along the same direction of the electric field.  However, the Hall Effect is an exception.  If you apply a magnetic field to a material, then the current may flow perpendicular to the electric field.

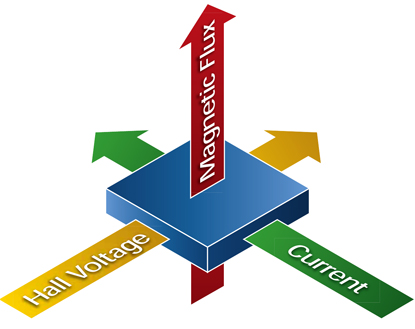
This horribly simplified image taken from here

If you apply a very strong magnetic field, you may create the Quantum Hall Effect.  Here, the current is an integer multiple of the physical constant h/e², times the voltage.  The “integer” part is what makes this interesting.  You end up with weird staircase graphs, like so:

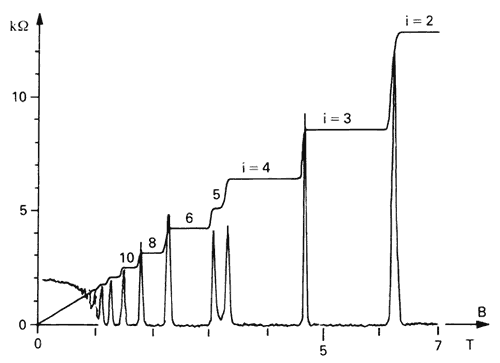
From the 1998 Nobel Prize.  The details aren’t important for my purposes.  However, I note that the staircase steps in this experiment are so precise, that they are used to measure the quantity h/e².

Haldane and Thouless contributed to this idea by showing the possibility of a quantum hall effect in a “Chern insulator” even without any magnetic field.  A Chern insulator was finally realized by experiments in 2013, 25 years after the theory had been proposed.

The Nobel Prize also credits Haldane for his work on quantum spin chains.

Suppose that we have a 1-dimensional wire, with a bunch of electrons in a chain.  Each electron has a spin, which can point either up or down.  It has long been known that this kind of system will never be ordered.  That is, you could never persuade all the electrons along the wire to point in the same direction, whereas you could in a 2-dimensional or 3-dimension magnet.

It was long assumed that this would also be true if instead of electron spin, we considered higher spins.  An electron has spin 1/2, and has only two quantum states, spin up or spin down (1/2 or -1/2).  But if you have a particle with spin 1, then it has more than two quantum states (1, 0, and -1).  Haldane showed that higher spins make a big difference, and that you can achieve an ordered 1-D system.  (This honestly surprises me, as I don’t remember that part being mentioned in my condensed matter courses.)

That’s all I got.  Further details can be found on the Nobel website.